Do We Need Pythagoras Here?
If lines l and m are parallel, then what is the value of angle x (in degrees)?
The answer is 35.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
57 solutions
1 2 5 = x + 9 0 , x = 3 5
In response to jonathan moey; Thank u another method is 125-90is 35
This is the exterior angle property I suppose?
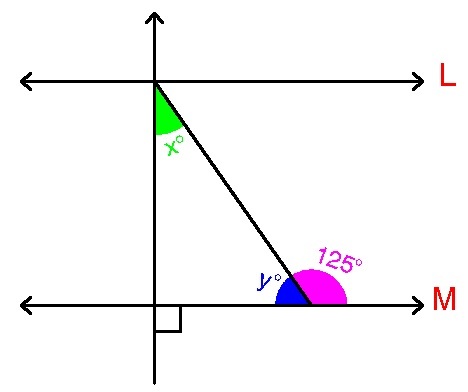 From my figure, since
y
and
1
2
5
∘
are supplementary angles, we have
From my figure, since
y
and
1
2
5
∘
are supplementary angles, we have
y + 1 2 5 = 1 8 0 ⟹ y = 1 8 0 − 1 2 5 = 5 5 ∘
Since the sum of the interior angles of a triangle is 1 8 0 , we have
x + y + 9 0 = 1 8 0 ⟹ x + 5 5 + 9 0 = 1 8 0 ⟹ x + 1 4 5 = 1 8 0 ⟹ x = 1 8 0 − 1 4 5 = 3 5
There is an alternate angle. The 125 is alternate to angle x + the 90degrees there as the lines L and P are perpendicular .
125+55=180 hence 90-55=35
sum of opposite interior angles=exterior angle n+90=125 n=125-90=35
Let m be the other angle in the triangle. This angle is supplementary with 125, therefore
1 2 5 + m = 1 8 0
m = 1 8 0 − 1 2 5 = 5 5
Also, line pv is perpendicular to vm, therefore, the angle in the triangle at v is 90. According to the angle sum theorem,
m + n + 9 0 = 1 8 0
n + 9 0 + 5 5 = 1 8 0
n = 1 8 0 − 1 4 5 = 3 5
there are two solutions the first is 125-90=35 and the second is 180-(55+90)=35
How I found the solution: First look at line m, and you see that you have 125 degrees and the other side is its supplement (Line M is Supplementary), which is 55 degrees. Then, you see the right angle, and you see that line v is perpendicular to line m which then tells you that this angle is 90 degrees. Therefore, 90 + 55 + X= 180 degrees x=35 degrees and that's how I got it.
n=180-( (180-125)+90) = 180-(55+90)=35
We know that half angle of the circle is 180 degree
On line 'm' outer angle is 125 degree. so, 180 - 125 = 55 degree (Which is inner angle now)
Since 'P' is perpendicular to 'm' the angle is 90 degree.
Now Remaining angle to find is 'x'
Total angle of triangle is = 180 degree ;
x = ? ;
Inner angle = 55 degree ;
Perpendicular angle = 90 degree ;
i.e., 180 = x + 90 + 55, 180 = x + 145, x = 180 - 145, x = 35
Why r u even trying so much Simple Its Exterior Angle Property 9 0 o + x = 1 2 5 o x = 1 2 5 o − 9 0 o x = 3 5 o
Log in to reply
When you are writing solutions to easier problems it is important to be explain your steps very clearly. It is obvious to those who know how to solve this type of problem, so a solution like yours would make sense, but someone who does not understand the problem would learn nothing from it.
Its easy method
1 8 0 ∘ − 1 2 5 ∘ = 5 5 ∘ by the rules of straight lines a ∘ + b ∘ = 1 8 0 ∘
9 0 ∘ − 5 5 ∘ = 3 5 ∘ by the right triangle rules a ∘ + b ∘ + 9 0 ∘ = 1 8 0 ∘ ⟹ a ∘ + b ∘ = 9 0 ∘
First 1 8 0 − 1 2 5 = 5 5 .Next we see that line m & line l are parallel so the third straight line are 9 0 ∘ to line m .So x + 9 0 + 5 5 = 1 8 0 ⟹ x = 1 8 0 − 9 0 − 5 5 = 1 8 0 − ( 9 0 + 5 5 ) = 1 8 0 − 1 4 5 = 3 5
The problem is overdetermined. It is does not matter whether lines m and l are parallel or not parallel. The exterior angle of a triangle of 125 degrees is equal to the sum of x and 90 degrees.
Two supplementary angles add up to 1 8 0 ∘ . The supplement of 1 2 5 ∘ is 1 8 0 − 1 2 5 = 5 5 ∘ . So the unknown angle is 9 0 − 5 5 = 3 5 ∘
We know that a straight line is consist of 180°.In the above picture we can see that one part of the line is 125°.So another part must be 180°-125°=55° Then x =180°-(55°+90°) =35°
In order to find m ∠ x , we must find the measure of the other two angles in our triangle.
This can be done by finding the measure of the angle adjacent to the m ∠ 1 2 5 angle:
1 8 0 − 1 2 5 = 5 5
Our second angle, which is adjacent to a right angle, must also be a right angle of 9 0 O .
Therefore, we can conclude that the measure of m ∠ x can be found by:
m ∠ x = ( 1 8 0 − ( 5 5 O + 9 0 O )
Where m ∠ x = ( 1 8 0 − ( 5 5 O + 9 0 O )
And m ∠ x = ( 1 8 0 − ( 1 4 5 O )
Therefore, m ∠ x = 3 5 O
Q ∙ E ∙ D
You see a 90 degree angel below the triangle, so that means that one of the angles of the triangle has to be a 90 degree angle, since l and m are parallel. The 125 degree angle only makes up a part of the 180 degree angle, so the other angle is 55 degrees. 90+55=145, and 180-145 is 35.
The given triangle is right angled triangle So x+90°=125° x=125°-90° x=35° This is the correct angle for x
No Pythogoras is not needed :)
We don't need Pythagoras here. Just the angles.A straight line forms 180 degree.If one angle is 125 degree,then remaining angle will be 180-125=55 degree. X is one of the angles of a triangle. 55 we found is also another angle of the same triangle.Opposite to the x is a perpendicular angle of the triangle.It forms angle of 90 degree.A triangle also forms the total of 180. Therefore, x+55+90=180 degree. x+145=180. x=180-145=35 degree.
Alternate interior angles are equal. So 120-90=35
Linear pair are supplementary, therefore 180-125=55 55+90=145 And since the sum of the angles of any triangle is 180 (180-145=35)
180-125=55 90+55=145 180-145=35
By exterior angle property 125-90=35
x degrees= 180-90-(180-125)= 35 degrees
Line M forms a 180 degrees since its a supplementary angle. We see that the right side is 125 degrees. We need to find the other side because we cannot solve for x without it. The left side is = 180 - 125 = 55 The second angle is 90 degree since it is perpendicular. We can now find the angle of x by adding the 2 angles - 180 degree (Any triangle has a sum of 180 degree) x = 180 - (55+90) = 35 degrees
External angle property SUM OF TWO INTERNAL ANGLES IS EQ TOVEXTERNAL ANGLE
Alternative interior angles in the parallel linens are equal So, 90 + X = 125 X = 125 - 90 X = 35
Is the problem from the book ( for class 9) of R.D. Sharma, isn't it ?
Since line p is perpendicular to point q, we can deduce that it creates a 90 degree angle. Since the angle with the measure of 125 and the angle inside the triangle create a linear pair, we can apply the linear pair postulate, which states that if twig angles form a linear pair, then they're supplementary. Supplementary angles have a sum of 180. To get the interior angle adjacent to the aforementioned angle, simply subtract 125 from 180, 180 — 125 = 55. We can add this to the other angle whichhas a measure of 90 degrees. Since all triangles have interior angles that sum up to 180, we can add the two angles and subtract it from 180 to get the measure of the last angle. 90+55=145. Subtract this from 180, 180—145=35. To check if this is correct, just add the measures of the interiors of the triangle and, if they equate to 180, your asnwer is correct. In this case, 90+55+35=180.
 Let A=n, B=90 deg.(because it is right angled triangle) and C=180-125(because angle formed on a st.line=180 deg.). Now we got B=90 degree and C=55 deg.. Therefore, A+B+C=180 deg. ; A+90+55=180; A+145=180; So, A=180-145=35 deg.
Let A=n, B=90 deg.(because it is right angled triangle) and C=180-125(because angle formed on a st.line=180 deg.). Now we got B=90 degree and C=55 deg.. Therefore, A+B+C=180 deg. ; A+90+55=180; A+145=180; So, A=180-145=35 deg.
Find the two angles of line M.
180-125= 55 Now find the missing angle in triangle. Triangle angles must equal 180. As a a right angle one of them is 90.
90-55= 35
180-125=55. 90+55=145. 180-145=35
"exterior angle is equal to sum of the interior opposite angles" is the theorem behind this..\
We know that in a triangle exterior angle is equal to the sum of opposite angles. therefore n+90=125 => n=125-90 => n=35 therefore n=35degrees
In the given fig, PQR (suppose R a point from P) forms a triangle. In triangle, PQR , exterior angle PQM = interior angle RPQ + interior angle PQR. ( exterior angle = sum of interior angles) so, 125 degree = x + 90 degree (PQ is perpendicular to m ) 125-90=x 35 degree = x
It seems that the total degrees of a triangle is equals to 180,and the adjacent angle of this is 125.Then this will be 180-125=55 and it seems that this is a right triangle so, 55 will be added to 90 for you to be able to get the remaining angle which is N=? so,55+90=145.Then my solution of this will be N=180-55-90 N=35.
180 - 125 = 55
90 - 55 = 35
125 is the same as n+90 because of the Z way of solving this because they are perpendicular lines. So then 125-90 is 35 (which is the real answer)
Since line l and line m are parrallel we have alternate interior angles. 125-90*=35 ……….. *90 degrees is from the perpendicular line f
180-125=55, then 55+90= 145...therefore 180-145=35... so 35 is the correct answer.
Easy. 180-125 to find the remaining angle which gives us 55. 55 is adjacent to the line L and P is perpendicular so its 90 and 90 + 55 gives us 145. Now that the whole angle equals 180. The angle remaining aka angle X would be 180-145 which gives us 35 which is our answer. Shaaf Farooq from Canada
Using the property that in a triangle the sum of 2 interior angles is equal to the exterior angle formed on the opposite side, solution can be found out as 90+x=125 => x=35
By the property of exterior angle which is equal to the sum of two opposite interior angle we can say that 90+x=125,Therefore x=35
125 degrees plus the angle adjacent must equal 180 degrees
180 - 125 = 55 degrees
The sum of all three angles within a triangle must be 180 degrees as well. Since we know line (p) is perpendicular to lines (l) and(m) that gives us our second angle where line (p) and (m) intersect, which is 90 degrees.
n= 180 - (90 + 55)
answer: angle (n) is 35 degrees.
l and m are parallel making angle 180-125=55 and at point q making 90 so 180-(55+90)=35
too easy question.. (180-125) = 55.......triangle = 180 deg......90+55+n = 180........n = 180-145......therefore n = 35
remember that the sum of the interior angles of a triangle is 180, Case solved.
There is a rule, if you have a triangle with angles A,B,C, and if there is an angle D such that C=180-D then D = A+B
You can do it the long way to prove this but it is easier to just memorize it :P
We know pq is a perpendicular. Since 125 is an external angle, x=125-90=35.
 y
∘
=
1
8
0
∘
−
1
2
5
∘
=
5
5
∘
y
∘
=
1
8
0
∘
−
1
2
5
∘
=
5
5
∘
x ∘ = 9 0 ∘ − 5 5 ∘ = 3 5 ∘

Since the straight lines n and m are perpedicular to each other, then the angle coloured in orange is a right angle.
On the straight line m , angles y ∘ and 1 2 5 ∘ must add up to 1 8 0 ∘ . So y ∘ + 1 2 5 ∘ = 1 8 0 ∘ or y ∘ = ( 1 8 0 − 1 2 5 ) ∘ = 5 5 ∘ .
The sum of angles in the triangle adds up to 180 degrees:
9 0 ∘ + x ∘ + 5 5 ∘ = 1 8 0 ∘ , x ∘ = ( 1 8 0 − 5 5 − 9 0 ) ∘ = 3 5 ∘
Hence, x equals 3 5 .