Lines and lines

There are three possibilities: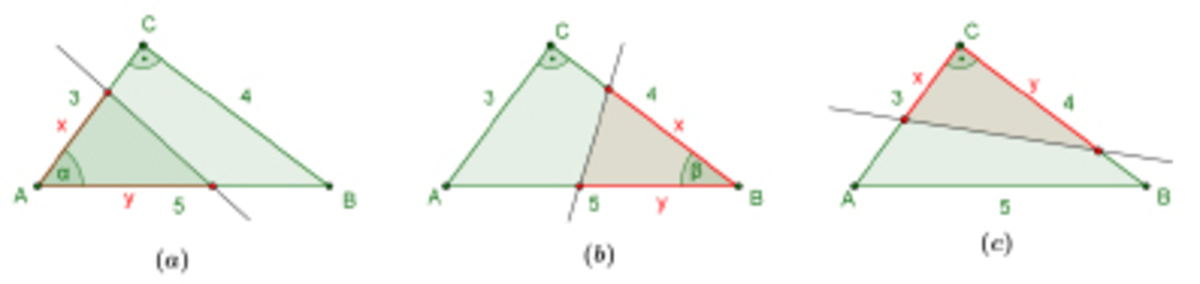

a) Hence $\begin{cases} x+y=6 \\ \frac{xy\sin \alpha}{2}=3 \end{cases}$ Using that $\sin\alpha =\dfrac{4}{5}$ we get that $\begin{cases} x+y=6 \\ xy=7.5\end{cases}$ The roots of it are: $\begin{aligned} x & = 3-\dfrac{\sqrt{6}}{2}\approx 1.78 \\ y & = 3+\dfrac{\sqrt{6}}{2}\approx 4.22\end{aligned}$ This gives us a solution.

b) Using $\sin\beta=\dfrac{3}{5}$ , we get $\begin{cases} x+y=6 \\ xy=10 \end{cases}$ which doesn't have any solutions.

c) Hence the cutted triangle is right angled, we get $\begin{cases} x+y=6 \\ xy=6 \end{cases}$ The roots of it $\begin{aligned} x & = 3-\sqrt{3}\approx 1.27 \\ y & = 3+\sqrt{3}\approx 4.73\end{aligned}$ Since $4.73$ is longer than both of the legs of the big triangle, this doesn't give us a solution.

Therefore there is exactly $\boxed{1}$ line, which satisfies the given conditions.