Liquid Friction!
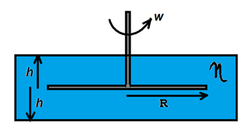 A Thin
circular
disk of radius
, rotates in a cylindrical chamber, which is filled with water (coefficient of viscosity
). It is rotated with
constant
angular velocity
.
A Thin
circular
disk of radius
, rotates in a cylindrical chamber, which is filled with water (coefficient of viscosity
). It is rotated with
constant
angular velocity
.
Find the
Power
developed (in
watts
)by the viscous forces, if the distance between the top-bottom walls and the disk is
.
Details and Assumptions:
Neglect end effects.
The answer is 178.945.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider an elemental ring of radius r in the disk. This elemental ring is moving with a velocity v = ω r in the liquid. The area of this element is d A = 2 π r d r . Now the liquid in contact with this elemental ring would also have the velocity of the same. So now by Newton's formula, the force on this ring is given by : d F = 2 h η A v = 2 h η w r 2 π r d r We can obtain the power due to this force ( P = F v ) , and on simplifying we get d P = h 4 π η ω 2 r 4 d r Integrating this result form r = 0 to R , we get the power developed as P = h π η ω 2 R 4 = 1 7 9 . 9 4 5