Liquid Planet!

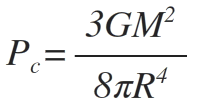
First, let's determine the gravitational find at a generic distance r from the center.

"Gauss's Law" for gravitation

$\int { \vec { g } \cdot \vec { dA } =4\pi G{ M }_{ enclosed } }$

Consider a concentric sphere with the planet (radius r, r<R) as our gaussian surface. "g" will be a constant along our integral, so itleaves the integral and we are left with an area integral(the surface area of the inner sphere).Then:

$g4\pi r²=4\pi GM\frac { r³ }{ R³ } \\ g=GM\frac { r }{ R³ }$

Now that we have g, let's try to adapt $P=\rho gh$ for this variable g situation. Consider a tiny column of liquid, with height dh exerting a pressure dP

$dP=\rho gdh=\rho gdr$

Pluggin the g we found and integrating both sides, we get: $dP=\rho GM\frac { r }{ R³ } dr\\ P=\frac { \rho GM }{ R³ } \int _{ 0 }^{ R }{ rdr } =\frac { \rho GM }{ 2R }$ Doing the math, $P=5.2E4$

When I looked at this question, it didn't really dawned on me that this problem belonged to the topic of Electricity and Magnetism. Thus, I applied a different way of doing using hydrostatic equilibrium concept to solve the problem.

An astronomical body is in a state of hydrostatic equilibrium (HE) when its self gravitational force is balanced by its internal pressure; the body is neither expanding nor contracting. From a technical perspective, a body in HE will assume a spherical shape to minimize gravitational potential since any deviations from sphericity increases gravitational energy. The size of deviations is affected by the body’s mass; the larger the mass, the smaller the deviations must be, all else being equal. However, its actual form depends on its rotation rate, mass, material strength, geologic activity and its history. The diagram below illustrates the balance between the two forces with an equation quantifying their magnitudes.

Diagram: Balance of Forces in Hydrostatic Equilibrium

Solving and simplifying the equation in the diagram to find the pressure in the center of the body in Hydrostatic equilibrium. It would be....

This interesting concept is taken from a research paper, check it out! Credits to the Hydrostatic Equilibrium concept

Nonetheless, I still prefer the derivation of the formula using Gauss law. Though I haven't grasp well on integration.