List them all?

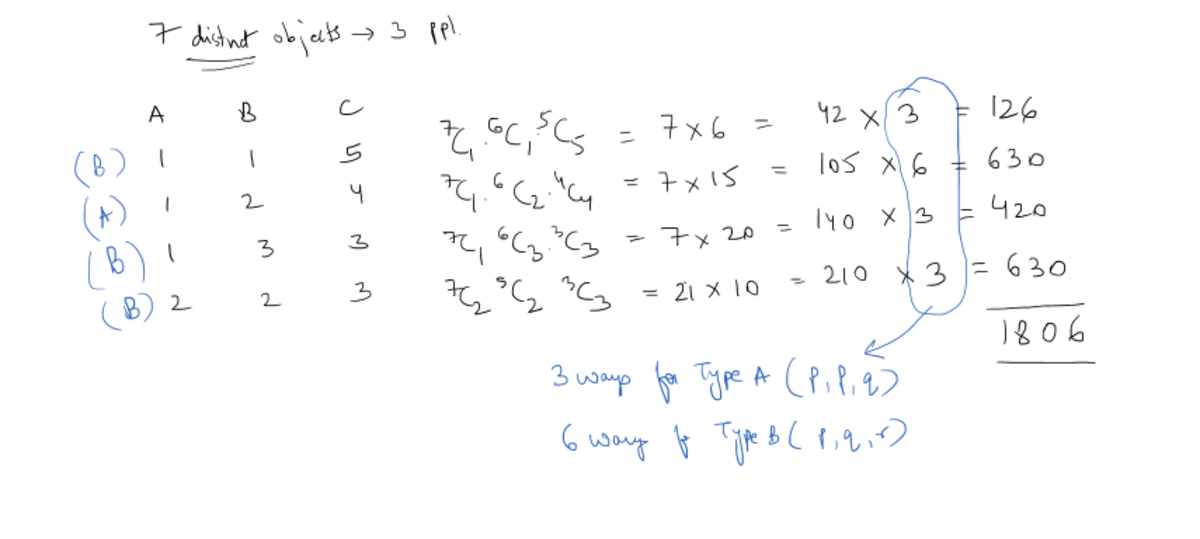
A quick way to solve this is with complementary counting. The problem asks for the number of ways where each person gets at least one object. We can find the answer by subtracting the number of ways where at least one person gets 0 objects from the total number of ways to distribute the objects.

The total number of ways to distribute the 7 objects is $3^7$ , since each object can be assigned to 3 possible people.

Now we find the number of ways where exactly one person gets 0 objects. Each object can be assigned to 2 possible people, so there are $2^7$ such possibilities, and there are ${3 \choose 1} = 3$ ways to choose the person that gets 0 objects. However, we have to subtract 2 from $2^7$ because it includes the 2 cases where all of the objects get assigned to one person (two people get 0 objects). So, the number of ways where exactly one person gets 0 objects is $3 \times (2^7-2)=378$ .

Now we find the number of ways where exactly two people get 0 objects. To get this, we are just choosing 1 person out of 3 people to get all of the objects. Therefore, there are $3$ such cases.

So, the answer is $\text{Total}-\text{Complement}=3^7-(378+3)=\boxed{1806}$ ways.

If that were three identical bags instead of three different people, that would be $\begin{Bmatrix}7\\3\end{Bmatrix}=301$ , the Stirling number of the second kind .

As the people are different and the object are distinct, we can multiply by the permutations of the three people.

$\begin{Bmatrix}7\\3\end{Bmatrix}·3!=301·6=\boxed{1806}$

$(3)^7-((2)^7×\binom{3}{2} -(1)^7×\binom{2}{1}×\binom{3}{2})-(1)^7×\binom{3}{1}=1806$

First term is the number of ways you can give 7 different objects to 3 people (1 or 2 people can get 0 objects).

Second term is the number of ways you can give 7 items to 2 people, multiplied by the number of ways to choose 2 people out of three.

The third term is the number of ways to give 7 objects to one person, multiplied by the number of ways to choose one person out of 2, multiplied by the number of ways to choose 2 people out of 3.

The last term is the number of ways you can give 7 objects to one person, multiplied by the number of ways to choose one person out of 3.

Well it can be done easily using inclusion exclusion principle.