Little Area
Showing a square with a side length of . An arc is drawn from center with a radius of and another arc is drawn from center with a radius . A little red circle is drawn in the white area which touches the two arc and the side of square, as shown in the diagram below
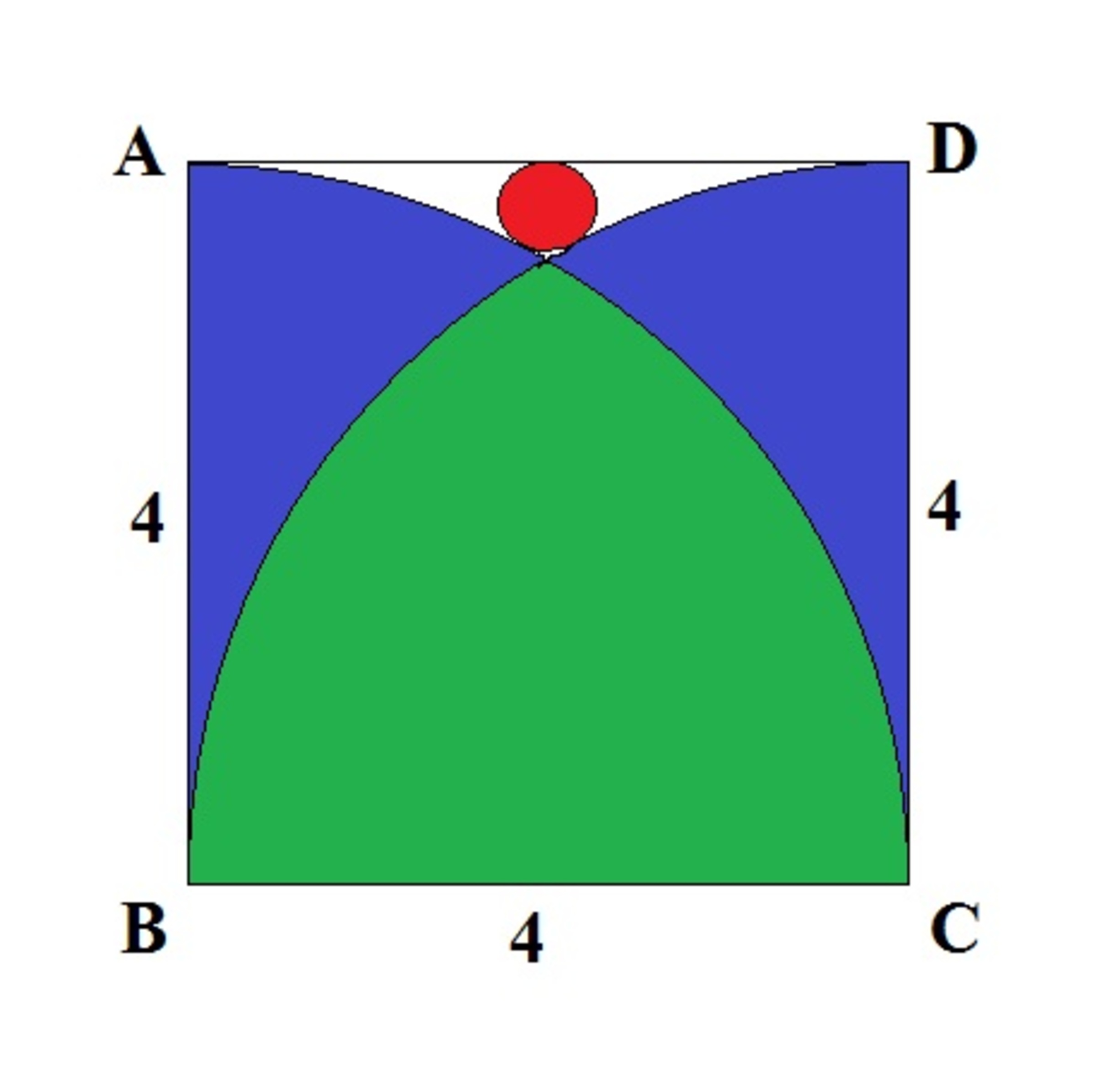
What's the area of circle?
[Give the answer in sq.cm unit.]
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A right triangle can be constructed where the hypotenuse is the segment joining the center of the little red circle and the center of one of the larger circles, as pictured below.
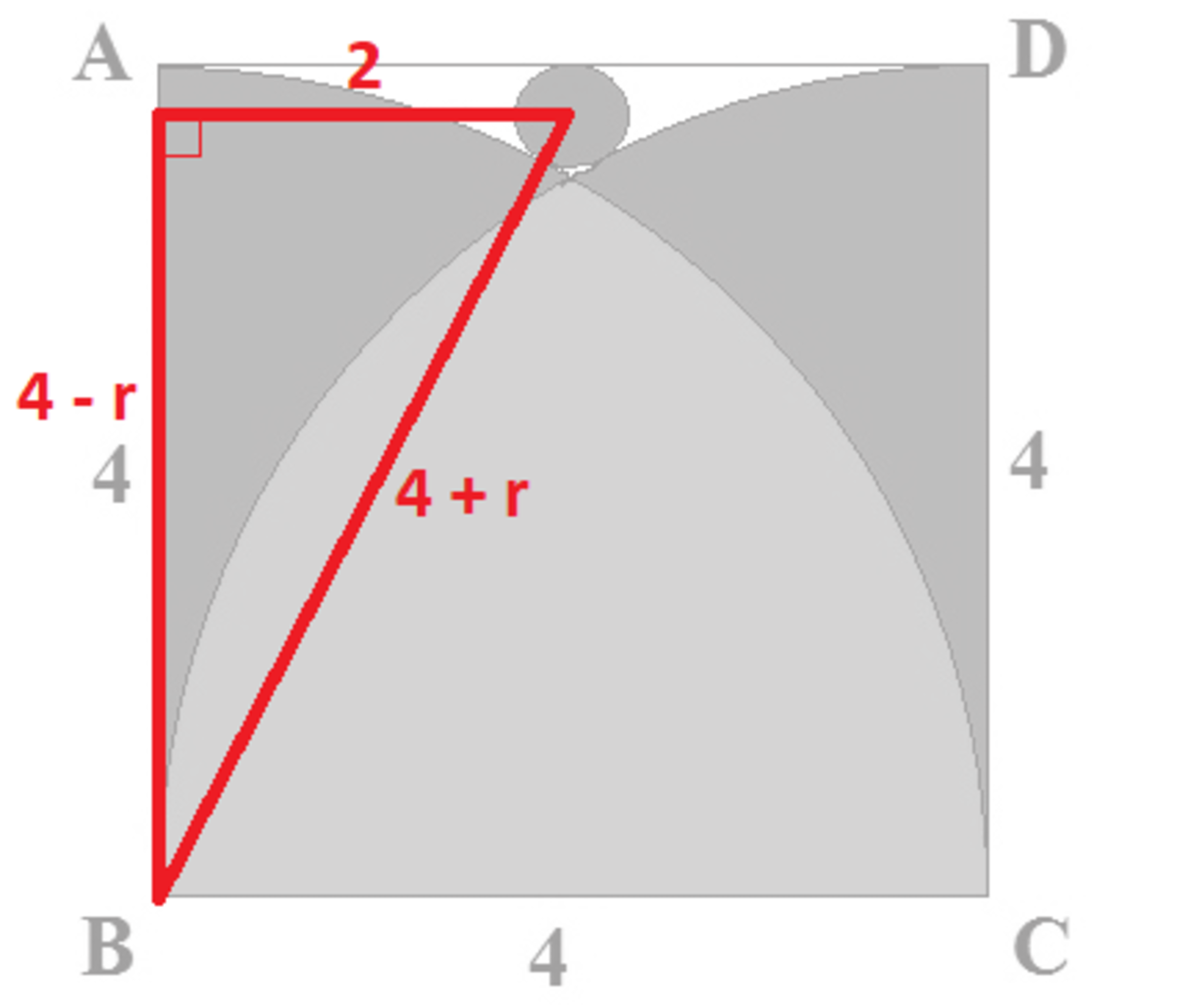
If the little red circle’s radius is r, then the hypotenuse is the sum of the two radii or 4 + r , the vertical leg is the difference of the two radii or 4 − r , and the horizontal leg is half the length of the square or 2 .
Using the Pythagorean Theorem gives ( 4 − r ) 2 + 2 2 = ( 4 + r ) 2 , and solving this gives r = 4 1 . The area of the little red circle must therefore be A = π r 2 = π ( 4 1 ) 2 = 1 6 π .