A geometry problem by Aaryan Maheshwari
What are all the possible perimeters of an isosceles triangle with sides of lengths 5 and 16?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Great visual of the triangle inequality :)
Great job on explaining this with a diagram!
Fooled me! I forgot to check for the second case! Shame!
Log in to reply
I would have too, if it hadn't given me the option of "Not possible to form a triangle"!
If the triangle is isosceles, then two of its sides should be equal. Thus, there are two possible perimeters: 5 + 5 + 1 6 = 2 6 u n i t s or 1 6 + 1 6 + 5 = 3 7 u n i t s . But according to the triangle inequality , 2 6 u n i t s cannot be a perimeter as 1 0 < 1 6 , that leaves the only choice, which is 3 7
Sir apply it like \ ( \ boxed { TEXT} \ )
WITHOUT LEAVING SPACES FOR BOXED ANSWER
Like x
OK. Thanks
Isosceles Triangles have 2 sides of equal length, so the possible sidelengths that we can form are 5 + 5 + 1 6 = 2 6 or 5 + 1 6 + 1 6 = 3 7 . But consider the scaled set-ups below: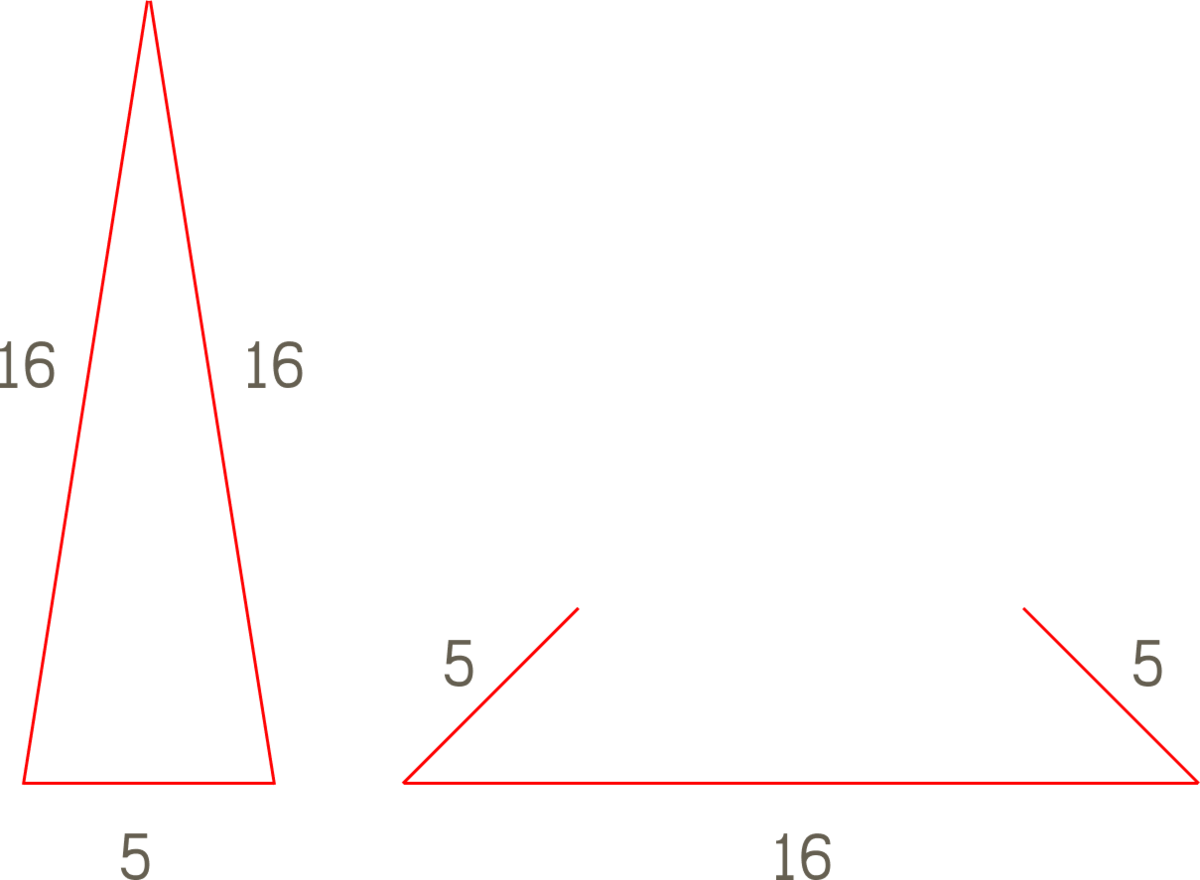 The sum of the two shorter lengths must be greater than that of the longest side. So we can rule out the possibility of
2
6
, leaving the answer of
3
7
.
The sum of the two shorter lengths must be greater than that of the longest side. So we can rule out the possibility of
2
6
, leaving the answer of
3
7
.