Fun House Mirror
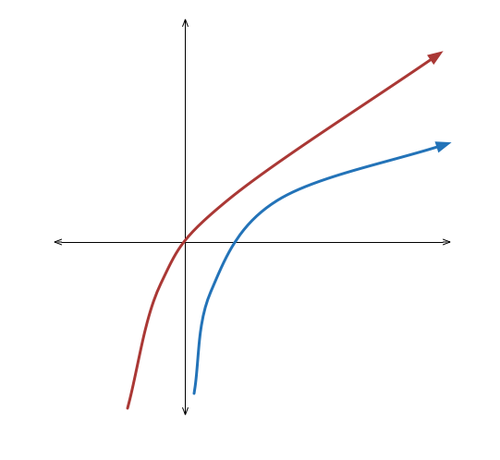 Given the graph
, which of these statements describes the transformations to get the graph of
for
?
Given the graph
, which of these statements describes the transformations to get the graph of
for
?
Translate to the left by 1 and up by , then scale vertically by 2.
Translate to the left by and up by , then scale vertically by 2.
Translate to the left by 1 and up by , then scale vertically by 2.
Translate to the left by and up by , then scale vertically by 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us work through the options
1) Translate the graph to the left by 1, translate the graph up by ln 4 , scale the graph vertically by 2.
The first transformation gives us y = ln ( x + 1 ) .
The second transformation gives us y = ln ( x + 1 ) + ln 4 .
The third transformation gives us y = 2 [ ln ( x + 1 ) + ln 4 ] = ln 1 6 ( x 2 + 2 x + 1 ) .
2) Translate the graph to the left by 2 1 , translate the graph up by ln 2 , scale the graph vertically by 2.
The first transformation gives us y = ln ( x + 2 1 ) .
The second transformation gives us y = ln ( x + 2 1 ) + ln 2 .
The third transformation gives us y = 2 [ ln ( x + 2 1 ) + ln 2 ] = ln ( 4 x 2 + 4 x + 1 ) .
3) Translate the graph to the left by 1, translate the graph up by ln 2 , scale the graph vertically by 2.
The first transformation gives us y = ln ( x + 1 ) .
The second transformation gives us y = ln ( x + 1 ) + ln 2 .
The third transformation gives us y = 2 [ ln ( x + 1 ) + ln 2 ] = ln ( 4 x 2 + 8 x + 4 ) .
4) Translate the graph to the left by 2 1 , translate the graph up by ln 4 , scale the graph vertically by 2.
The first transformation gives us y = ln ( x + 2 1 ) .
The second transformation gives us y = ln ( x + 2 1 ) + ln 4 .
The third transformation gives us y = 2 [ ln ( x + 2 1 ) + ln 4 ] = ln ( 1 6 x 2 + 1 6 x + 4 ) .
Hence, the answer is 2) Translate the graph to the left by 2 1 , translate the graph up by ln 2 , scale the graph vertically by 2.
Note: For the full graph of y = ln ( 4 x 2 + 4 x + 1 ) , we will also need to reflect it with respect to the line x = − 2 1 . The reason for this is that
y = ln ( 4 x 2 + 4 x + 1 ) = 2 [ ln 2 + ln ∣ x + 2 1 ∣ ] .