Local Extrema Count

Calculus Level 2

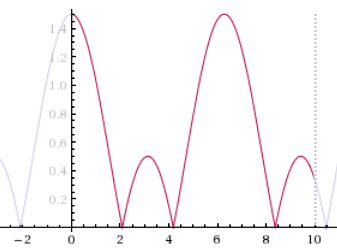
The graph at right depicts the function $\color{darkred}{f(x)} = |\cos x + 0.5|$ in the interval $\color{darkred}0 \leq \color{darkred}x \leq \color{darkred}{10}$ .

How many local extrema does the function $f(x)$ have if its domain is restricted to ${\color{darkred}0 \leq \color{darkred}x \leq \color{darkred}{10}}?$

3 4 5 6 7 8 Infinitely many

1 solution

Zandra Vinegar Staff
Dec 24, 2015

There are 8 local extrema: 4 local maxima and 4 local minima.

Proof:

Definition: a local extremum of $f(x)$ is a point, $P = (p, f(p))$ such that there is a small interval of $f(x)$ immediately around $P$ , such that $f(p) > f(x)$ for all $x \neq p$ in that interval.

there is no such interval around x=0 and x=10. since the domain is restricted in 0=< x =< 10, if it would have an interval around these points then it would include points smaller than 0 and greater than 10; that is, points that are outside of the given domain. so the solution are the six other points and the answer becomes 6.

Gabriel Rakaj - 4 years, 5 months ago

I feel the same thing.

Sumant Chopde - 2 years, 2 months ago

The definition I learned is that it has a minimum at x=c if f(x)>=f(c) for values sufficiently close to c from both sides . Based on that I agree with you, though it is possible that my definition is incorrect.

Nathan Henry - 1 year, 11 months ago

Seems the definition given above for the proof is only for the local max. I also agree with Gabriel Rakaj as I only see 6 local extrema since the endpoints are not local. I ask Zandra Vinegar or any other staff member to please reply to either correct my understanding or to modify the quiz to avoid future confusion if that is warranted. Thanks!

Scott Tuttle - 1 year, 6 months ago

Local Extrema Count

1 solution

0 pending reports