Locate The A B
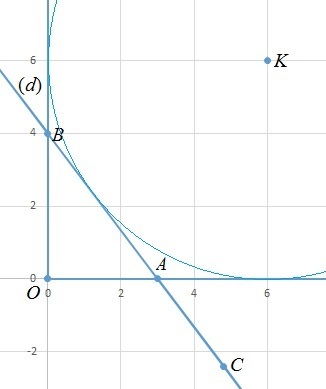
The following figure shows a triangle O A B in the x y -plane, with point O the origin and point A , B ∈ ( d ) whose equation is 4 x + 3 y − 1 2 = 0 . Point K ( 6 ; 6 ) is the excenter of O . Point C ( 5 2 4 ; − 5 1 2 ) ∈ ( d ) so that A C = A O and point A lies between points C and B .
If the coordinates of points A and B can be represented as ( x a ; y a ) and ( x b ; y b ) respectively, find x a + y a + x b + y b .
Note: The above figure is not drawn to scale
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
The distance from K ( 6 , 6 ) to the line 4 x + 3 y − 1 2 = 0 is given by 4 2 + 3 2 ∣ 4 ⋅ 6 + 3 ⋅ 6 − 1 2 ∣ = 6 , which is also the radius of the circle.
Since the center of the circle is K ( 6 , 6 ) , and its radius is 6, it is tangent to both the x -axis and y -axis. Thus, A and B are the x -intercept and the y -intercept of the line 4 x + 3 y − 1 2 = 0 , in some order. The x -intercept is (3,0) and the y -intercept is (0,4), so the answer is 3 + 0 + 0 + 4 = 7 .
Note that information about point C is never used, so it is not needed.
No need to find distance between d and K. Since it is the r_o, which is 6.
A lies on perpendicular bisector of OC as well as on line d. Solve the two equations to get A(3,0).
Now, reflect A about line OK to get point X. Note that this point X lies on line segment OB. Hence find equation of OB. Solve it with equation of line d to get B(0,4)
Good one, much quicker to find B
But you need to prove that such point X lies on OB ^^
Log in to reply
That is very easy to show and a very elementary property in geometry. Hence, I did not mention that.. Just use congruence of triangles to prove it....
(See above figure for details)
There are a few approaches to this problem but this is one i have come up with.
First we need to find some geometric proofs.
Let point D ∈ ( d ) so that B O = B D and point B lies between points A and D . Let E = A K ∩ O C , F = B K ∩ O D and K H ⊥ ( d ) with H ∈ ( d ) .
Since point K is the excenter of O so K E is the bisector of ∠ O A C . We also have Δ O A C is an isosceles triangle so we can imply that point E is the midpoint of O C and K C = K O .
Similarly, point F is the midpoint of O D and K D = K O .
We have K C = K O = K D so Δ C K D is an isosceles triangle. Therefore, point H is the midpoint of C D .
Then, let's take these proofs into the coordinates system.
We have had the coordinates of point O and C so we can find the coordinates of midpoint E of O C that is ( 5 1 2 ; 5 − 6 ) . Line segment E K ⊥ O C and passes point E so its equation is 2 x − y − 6 = 0 .
We have A = E K ∩ ( d ) and both line equations have been found so we can find the coordinates of point A that is ( 3 ; 0 )
We have line segment K H ⊥ ( d ) and passes point K so its equation is 3 x − 4 y + 6 = 0 . We also have point H = K H ∩ ( d ) so its coordinates is ( 5 6 ; 5 1 2 ) . Since we have proved that H is the midpoint of C D so we can find the coordinates of point D that is ( 5 − 1 2 ; 5 3 6 )
By the same way that we have found the coordinates of point A , we can find the coordinates of point B that is ( 0 ; 4 ) .
In conclusion, x a + y a + x b + y b = 7
T h e l i n e d i s 3 X + 4 Y = 1 . S o X a n d Y i n t e r s e c t s a r e 3 a n d 4 . K i s o n Y = X , t h a t b i s e c t s t h e r i g h t ∠ t h r o u g h O , ∴ A a n d B a r e e a c h o n o n e o f t h e a x i s . C i s n e a r A , a n d i n f o u r t h q u a d r a n t . ∴ A , i s a t i n t e r s e c t i o n o f Y = 0 a n d d , ∴ A ( 3 , 0 ) = ( X a , Y a ) . S i m i l a r l y B ( 0 , 4 ) = ( X b , Y b ) . ∴ X a + Y a + X b + Y b = 3 + 0 + 0 + 4 = 7 .
Since A C = A O , we have:
A C 2 ( x a − 5 2 4 ) 2 + ( y a + 5 1 2 ) 2 x a 2 − 5 4 8 x a + 2 5 5 7 6 + y a 2 + 5 2 4 y a + 2 5 1 4 4 − 5 4 8 x a + 5 2 4 y a + 2 5 7 2 0 − 4 x a + 2 y a + 1 2 3 y a − 1 2 + 2 y a + 1 2 ⟹ y a x a = A O 2 = ( x a − 0 ) 2 + ( y a − 0 ) 2 = x a 2 + y a 2 = 0 = 0 = 0 = 0 = 3 Note that 4 x a + 3 y a − 1 2 = 0
Therefore, A ( 0 , 3 ) is on the x -axis and O A is along the x -axis. Excircle centered at K is hence tangent to the x -axis and has a radius of 6 and since the excenter K is at ( 6 , 6 ) the excircle is also tangent to the y -axis as shown in the figure below. Implying that the line O B is along y -axis and x b = 0 , ⟹ y b = 4 .
Therefore, x a + y a + x b + y b = 3 + 0 + 0 + 4 = 7 .