Locus and area
Let L be the set of lines that are tangent to the curve y = x 2 + 4 1 .
Construct curve C by reflecting origin O across every element of L .
Area of the region enclosed by C is equal to a − b π , where a and b are rational numbers.
Evaluate b a .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
A bit of a sketch solution but the missing derivations are easy to check.
The image of the origin reflected in the line a x + b y + c = 0 has coordinates ( a 2 + b 2 − 2 a c , a 2 + b 2 − 2 b c ) .
The tangent to the curve L at the point P ( t , t 2 + 4 1 ) has equation 2 t x − y + 4 1 − t 2 = 0 .
Putting these two together, we find the curve C is defined parametrically by
x y = t ⋅ 4 t 2 + 1 4 t 2 − 1 = − 2 1 ⋅ 4 t 2 + 1 4 t 2 − 1
Noting the similarity with the tangent-half angle substitution formulas , we put 2 t = tan θ to get
x y = − 2 1 cos 2 θ tan θ = 2 1 cos 2 θ
The next useful observation is that
sin θ x cos θ y = − 2 1 cos 2 θ sec θ = 2 1 cos 2 θ sec θ
so the curve in question can be obtained from the polar curve C ′ : r = 2 cos ϕ cos 2 ϕ by applying a rotation through 9 0 ∘ .
This transformation does not affect the enclosed area of C ′ (which lies in the interval − 4 π ≤ ϕ ≤ 4 π ), so the required area (using the standard formula for areas in polar coordinates) is given by
∫ − 4 π 4 π 2 1 r 2 d ϕ = ∫ − 4 π 4 π 2 1 ( 2 cos ϕ cos 2 ϕ ) 2 d ϕ = ∫ − 4 π 4 π 8 1 cos 2 ϕ ( 2 cos 2 ϕ − 1 ) d ϕ = ∫ − 4 π 4 π 8 1 cos 2 ϕ 4 cos 4 ϕ − 4 cos 2 ϕ + 1 d ϕ = ∫ − 4 π 4 π 8 1 ( 4 cos 2 ϕ − 4 + sec 2 ϕ ) d ϕ = 2 1 − 8 π
and the final answer is 4 .
Does anyone know the name of this curve? It looks similar to (but isn't) the folium of Descartes and the trisectrix of Maclaurin. Also, is there a name for the curve generated via this type of reflection?
Several typos. (i) y = 2 1 . 1 + 4 t 2 1 − 4 t 2 .
(ii) t = 2 1 tan θ .
Log in to reply
Thanks! Corrected now. I'm not all that happy with this solution - it seems a bit over-complicated. Did you happen to find a better way?
Sir, in blue in the figure below is the plot of the curve (we both found the same parametric expressions), and in red is a rectagle going from − ( 2 − 2 π ) to ( 2 − 2 π ) and of height equal to 0 . 5 , i.e., a rectangle with area ( 2 − 2 π ) .
Notice that the area of the rectangle is greater than the area of the curve, which actually is 2 1 − 8 π . The stretching by 2 and 2 1 do make a difference. The ratio b a will be the same, but a and b themselves will be different.
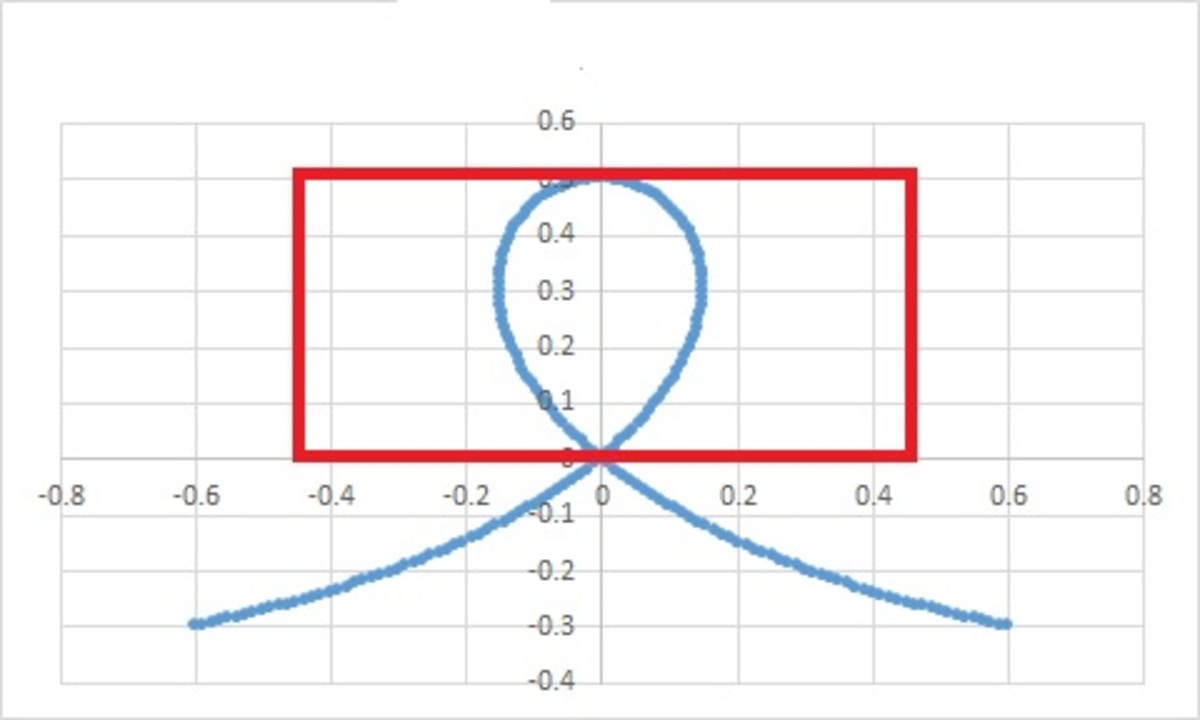
Log in to reply
Ah, thanks, I found my mistake. No need for stretching at all!
I've found a solution slightly different than mr @Chris Lewis. Here it is:
Since the derivative of y = x 2 + 4 1 with respect to x is equal to 2 x , the tangents to the curve in a point ( t , t 2 + 4 1 ) will have equation:
y − ( t 2 − 4 1 ) = ( 2 t ) ⋅ ( x − t )
y = 2 t x − t 2 + 4 1
The line which is perpendicular to the aforementioned tangent line and passes to the origin must have inclination equal to the negative inverse inclilation of the line and constant term equal to 0. So:
y = − 2 t 1 x
The point P ( x P , y P ) of intersection among those lines is found by:
2 t x − t 2 + 4 1 = − 2 t 1 x
x P = 2 ( 4 t 2 + 1 ) 4 t 3 − t
y P = 4 ( 4 t 2 + 1 ) − 4 t 2 + 1
Each point of C will then be given by 2 times vector O P :
x = 4 t 2 + 1 4 t 3 − t
y = 2 ( 4 t 2 + 1 ) − 4 t 2 + 1
This curve passes through ( 0 , 0 ) when t = − 0 . 5 , goes to ( 0 , 0 . 5 ) when t = 0 and then goes back to ( 0 , 0 ) when t = 0 . 5 , enclosing an area. The integral we're looking for is then:
A = ∣ ∣ ∣ ∣ ∣ ∫ y d x ∣ ∣ ∣ ∣ ∣
A = ∣ ∣ ∣ ∣ ∣ ∫ − 0 . 5 0 . 5 y ( d t d x ) d t ∣ ∣ ∣ ∣ ∣
A = ∣ ∣ ∣ ∣ ∣ 2 1 ∫ − 0 . 5 0 . 5 ( 4 t 2 + 1 ) 3 − 6 4 t 6 − 4 8 t 4 + 2 0 t 2 − 1 d t ∣ ∣ ∣ ∣ ∣
The reason for the absolute value is that the integral itself can be positive or negative depending on the orientation chosen, but an area must be positive. Expanding in partial fractions:
A = ∣ ∣ ∣ ∣ ∣ 2 1 ( ∫ − 0 . 5 0 . 5 [ ( 4 t 2 + 1 ) 2 8 − ( 4 t 2 + 1 ) 3 8 − 1 ] d t ) ∣ ∣ ∣ ∣ ∣
A = ∣ ∣ ∣ ∣ ∣ 2 1 ( ∫ − 0 . 5 0 . 5 [ ( 4 t 2 + 1 ) 2 8 − ( 4 t 2 + 1 ) 3 8 ] d t − 1 ) ∣ ∣ ∣ ∣ ∣
And then making t = 2 tan ( u ) , one gets:
A = ∣ ∣ ∣ ∣ ∣ ∣ 2 ⎝ ⎛ ∫ − 4 π 4 π ( cos 2 ( u ) − cos 4 ( u ) ) d u ⎠ ⎞ − 2 1 ∣ ∣ ∣ ∣ ∣ ∣
Since cos ( 4 u ) = 8 cos 4 ( u ) − 8 cos 2 ( u ) + 1 , then cos 2 ( u ) − cos 4 ( u ) = 8 1 ( − cos ( 4 u ) + 1 ) . Then:
A = ∣ ∣ ∣ ∣ ∣ ∣ 2 ⎝ ⎛ 8 1 ∫ − 4 π 4 π ( − cos ( 4 u ) + 1 ) d u ⎠ ⎞ − 2 1 ∣ ∣ ∣ ∣ ∣ ∣
A = ∣ ∣ ∣ ∣ ∣ ∣ 4 1 ( − 4 sin ( 4 u ) + u ) − 4 π 4 π − 2 1 ∣ ∣ ∣ ∣ ∣ ∣
A = 2 1 − 8 1 π
So:
a = 2 1 , b = 8 1 → b a = 4