Locus of Circumcenters

Geometry Level 5

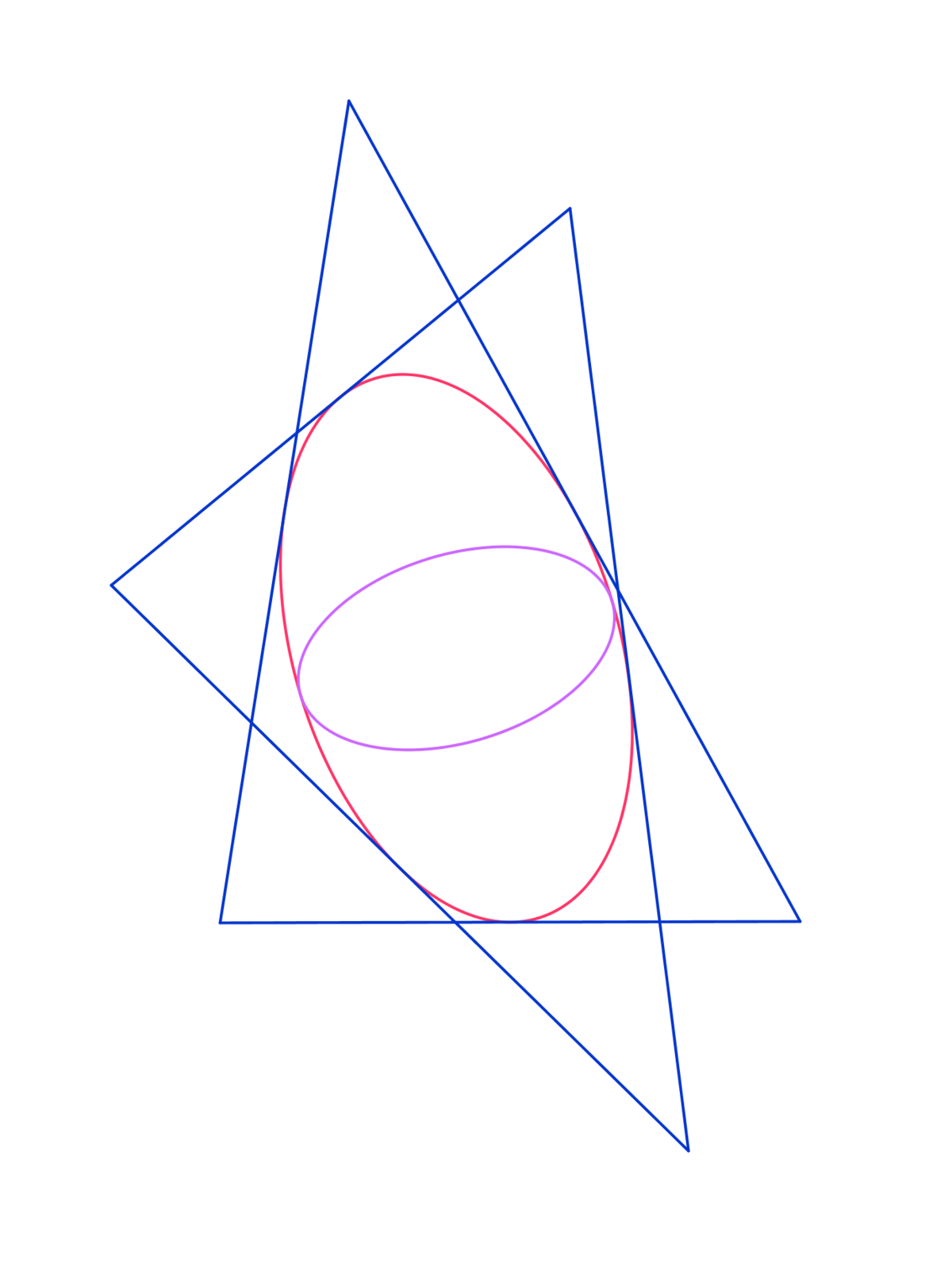
There is an ellipse $d$ with semi-major axis $a$ and semi-minor axis $b$ . There is another ellipse $e$ inscribed inside ellipse $d$ with two points tangent.

For all the triangles $T_i$ for which $d$ is Steiner inellipse, $e$ is locus of their circumcenters.

Find $\left(\dfrac{a}{b} \right)^2$ .

The problem is original

The answer is 3.

1 solution

Maria Kozlowska
Feb 5, 2016

We can start off with isosceles right triangle, reflect its vertices around centroid and create Steiner circum-ellipse going through all 6 points, then dilate it around centroid by factor of $\frac{1}{2}$ to get Steiner innelipse. Steiner circumellipse dilated by a factor of $\frac{1}{\sqrt{3}}$ and rotated by 90 degrees around centroid will give locus of all orthocentres. Orthocentre of our right triangle coincides with its point of tangency with Steiner circum-circle. The last step will be to dilate that ellipse by a factor of $\frac{1}{2}$ to get locus of all circumcentres. Please note that circumcenter distance to centroid is half the distance of orthocentre to centroid on the euler line . All the ellipses mentioned have same proportion of their semi-axes which is $\sqrt{3}$ which gives answer of $\boxed{3}$ .

The key to solving this one is to recognize that for the circumcenter of an isosceles triangle to be right on the side is for the isosceles triangle to be a right angled one. So, we scale an equilateral triangle with an inscribed circle in one direction by a factor of $\frac{1}{\sqrt{3}}$ to get the ellipse we want. With $a$ being the major semi-axis, we find that $a:b=\sqrt{3}:1$ , and we have our answer.

Michael Mendrin - 5 years, 4 months ago

Locus of Circumcenters

The problem is original

The answer is 3.

1 solution

0 pending reports