Locus of the Symmedian

Geometry Level pending

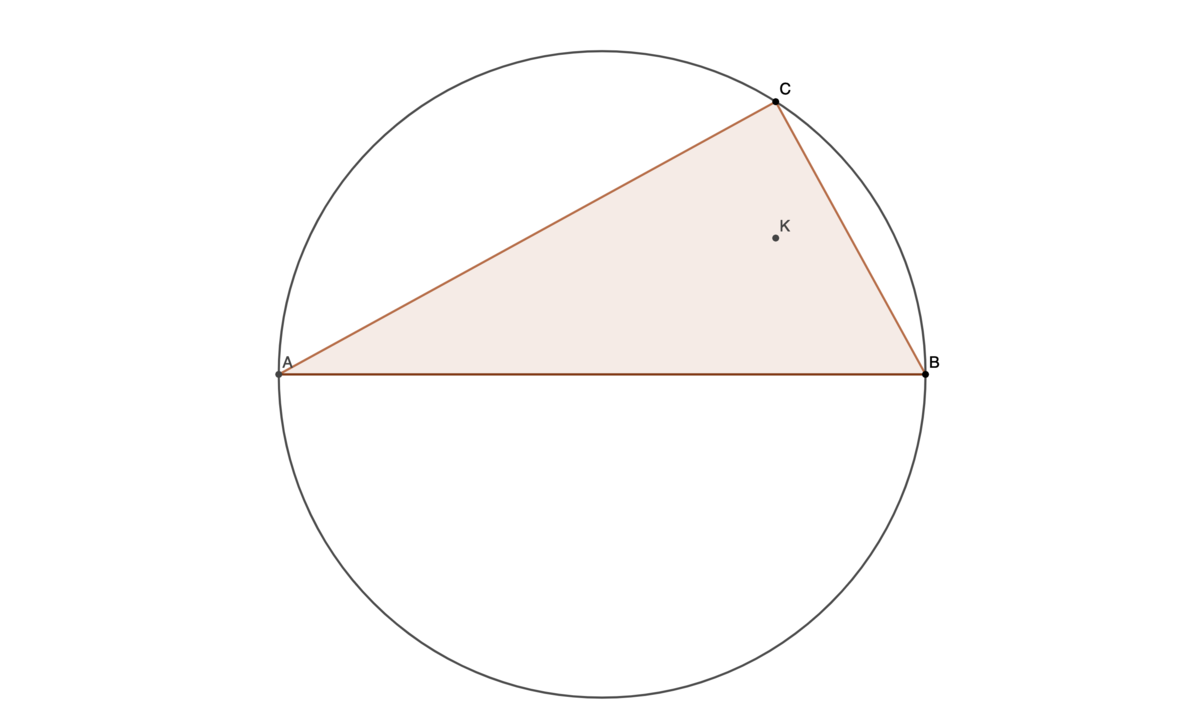
$\triangle ABC$ is inscribed in the unit circle. $AB$ is a diameter of the circle. $K$ is the symmedian point of $\triangle ABC$ . $C$ is free to move on the circumference of the circle. Find the area enclosed by the locus of $K$ as $C$ makes a complete revolution around the circle.

The answer is 1.57.

1 solution

Hosam Hajjir
Mar 2, 2021

The symmedian point for a right triangle is the located at the midpoint of the altitude from the right angle to the hypotenuse. Since the locus of $C$ is a circle with radius $1$ , the locus of $K$ is an ellipse with semi-axes $1$ and $\dfrac{1}{2}$ , therefore, its area is $\dfrac{\pi}{2}$ .

Locus of the Symmedian

The answer is 1.57.

1 solution

0 pending reports