Locus-Pocus
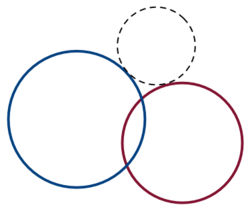 Two non-congruent circles
and
intersect at two distinct points. The locus of the centers of all circles tangent to both
and
is...
Two non-congruent circles
and
intersect at two distinct points. The locus of the centers of all circles tangent to both
and
is...
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let Λ be the circle tangent to both Γ 1 and Γ 2 . Also let r 1 and r 2 be the radii of Γ 1 and Γ 2 , respectively, and let x be the radius of Λ . Finally, let G 1 and G 2 be the centers of Γ 1 and Γ 2 , respectively, and let L be the center of Λ .
There are four cases to consider.
Case 1: Λ is inside both Γ 1 and Γ 2
In this case, ∣ G 1 L − L G 2 ∣ = ∣ ( r 1 − x ) − ( r 2 − x ) ∣ = ∣ r 1 − r 2 ∣ , which is constant.
Case 2: Λ is outside both Γ 1 and Γ 2
In this case, ∣ G 1 L − L G 2 ∣ = ∣ ( r 1 + x ) − ( r 2 + x ) ∣ = ∣ r 1 − r 2 ∣ , the same constant as in Case 1 above. Therefore, in both Case 1 and Case 2 , the center L lies on a hyperbola whose foci are G 1 and G 2 .
Case 3: Λ is inside Γ 1 but outside Γ 2
In this case, G 1 L + L G 2 = ( r 1 − x ) + ( r 2 + x ) = r 1 + r 2 , which is constant.
Case 4: Λ is outside Γ 1 but inside Γ 2
In this case, G 1 L + L G 2 = ( r 1 + x ) + ( r 2 − x ) = r 1 + r 2 , the same constant as in Case 3 above. Therefore, in both Case 1 and Case 2 , the center L lies on an ellipse whose foci are G 1 and G 2 .
I realize that this is not a complete/rigorous proof, but there's enough there to make "an ellipse and a hyperbola" at least the best answer among the choices given!