This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
loga b = 1/logb a
1.log3 24 x log 3 72 - log3 216 x log3 8
2.log3 (8x3) x log3 72 - log3 (8 x 3^3) x log3 8
3.(log3 8 + 1 ) x (log3 8 + 2) - (log3 8 + 3 ) (log3 8)
4.let log3 8 be x
5.(x+1) (x+2 ) - (x+3) (x)
6.x^2 +2x + x +2 - x^2 - 3x =2
convert everything in form of ( lo g 3 8 )
the expression becomes
[ ( lo g 3 ( 8 ∗ 3 ) ) ∗ ( lo g 3 ( 8 ∗ 3 2 ) ) ] − [ ( lo g 3 ( 8 ∗ 3 3 ) ) ∗ ( lo g 3 ( 8 ) ) ]
the simplified expression is
[ ( lo g 3 8 + 1 ) ∗ ( lo g 3 8 + 2 ) ] − [ ( lo g 3 8 + 3 ) ∗ ( lo g 3 8 ) ]
now take ( lo g 3 8 ) = a
the expression becomes
( a + 1 ) ( a + 2 ) − ( a + 3 ) ( a ) )
= a 2 + ( 3 ∗ a ) + 2 − a 2 − ( 3 ∗ a )
= 2
Bearing in mind the identity Brian made reference to in his working, we can rewrite the expression to be:
l o g 3 2 4 l o g 3 7 2 − l o g 3 2 1 6 l o g 3 8 = l o g 3 2 4 ( l o g 3 7 2 ) − ( l o g 3 ( 7 2 × 3 ) ) ( l o g 3 3 2 4 )
= l o g 3 2 4 ( l o g 3 7 2 ) − ( l o g 3 7 2 + 1 ) ( l o g 3 2 4 − 1 ) = l o g 3 7 2 − l o g 3 2 4 + 1
= l o g 3 2 4 7 2 + 1 = l o g 3 3 + 1 = 1 + 1 = 2
just use base change property , assume log2 base 3 to be equal to a x and then just simplify , then x will get cancelled and 2 will remain. So Ans=>2
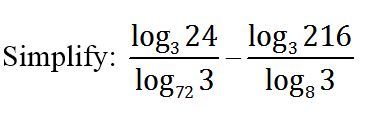
Note first that in general lo g a b = lo g b a 1 for a , b > 0 .
So the expression becomes
lo g 3 ( 3 ∗ 8 ) ∗ lo g 3 7 2 − lo g 3 ( 3 ∗ 7 2 ) ∗ lo g 3 8 =
( 1 + lo g 3 8 ) ∗ lo g 3 7 2 − ( 1 + lo g 3 7 2 ) ∗ lo g 3 8 =
lo g 3 7 2 − lo g 3 8 = lo g 3 8 7 2 = lo g 3 9 = 2 .