Logarithm Basics Part IV

Algebra Level 4

$\large \color{#3D99F6}{\log_3(9^x+9)=x+\log_3(28-2 \cdot 3^x)}$

If $a_1,a_2,...a_n$ are the real roots of the above equation, then find the value of $\dfrac{a_1+a_2+...+a_n}{n}$

Join the Brilliant Classes and enjoy the excellence.

The answer is 0.5.

2 solutions

Brian Charlesworth
May 11, 2015

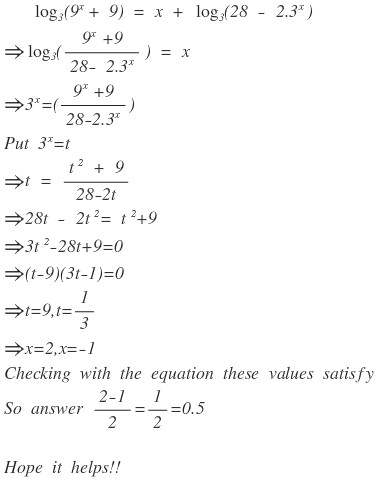
This equation can be rewritten as

$\log_{3}(9^{x} + 9) = \log_{3}(3^{x}) + \log_{3}(28 - 2*3^{x})$

$\Longrightarrow \log_{3}(9^{x} + 9) = \log_{3}(3^{x}(28 - 2*3^{x})).$

Now as the log function is one-to-one we can equate arguments to find that

$(3^{2})^{x} + 9 = 3^{x}(28 - 2*3^{x}) \Longrightarrow (3^{x})^{2} + 9 = 28*3^{x} - 2*(3^{x})^{2}$

$\Longrightarrow 3*(3^{x})^{2} - 28*3^{x} + 9 = 0,$

which is quadratic in $3^{x}$ with solutions

$3^{x} = \dfrac{28 \pm \sqrt{28^{2} - 4*3*9}}{2*3} = \dfrac{28 \pm 26}{6} = \dfrac{14 \pm 13}{3}.$

We thus have that either $3^{x} = \dfrac{14 + 13}{3} = 9 \Longrightarrow x = 2$ or

$3^{x} = \dfrac{14 - 13}{3} = \dfrac{1}{3} \Longrightarrow x = -1.$

The reader can confirm that both these values of $x$ satisfy the original equation. Thus the desired solution is $\dfrac{2 + (-1)}{2} = \boxed{0.5}.$

while solving quadratic equation in $3^x$ you can assume it like $a=3^x$ . it will easy the solution

Dhirendra Singh - 6 years, 1 month ago

Ravi Dwivedi
Jul 5, 2015

Moderator note:

Simple standard approach for solving such logarithm equations.

Always remember to check that the solutions do indeed satisfy the original equation. The sequence of steps are not if and only if because we cannot take the logarithm of a negative number.

Logarithm Basics Part IV

Join the Brilliant Classes and enjoy the excellence.

The answer is 0.5.

2 solutions

Moderator note:

0 pending reports