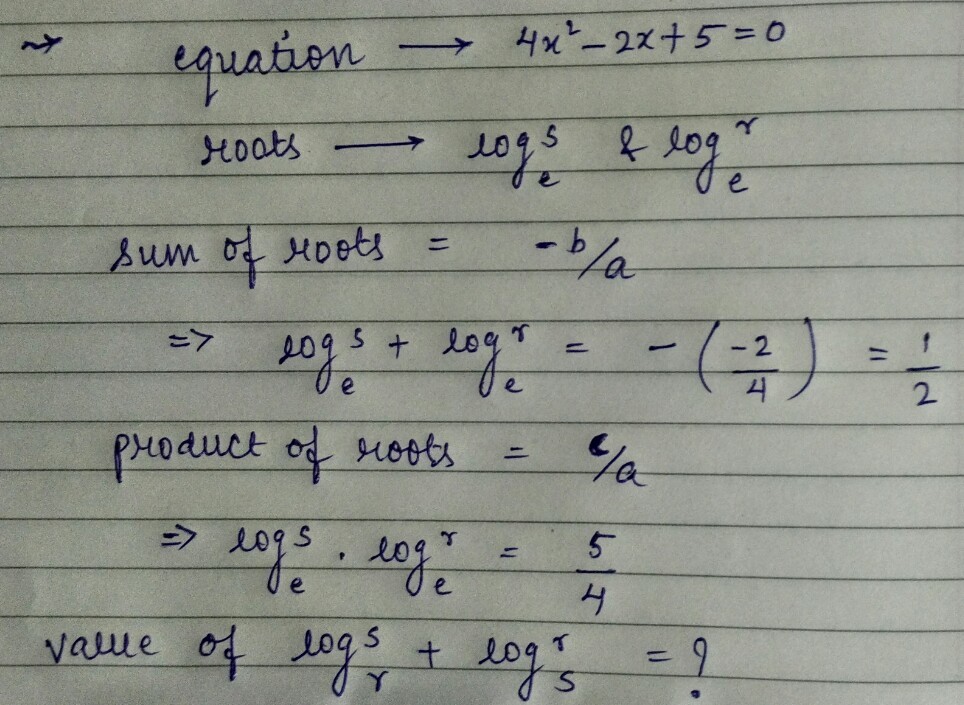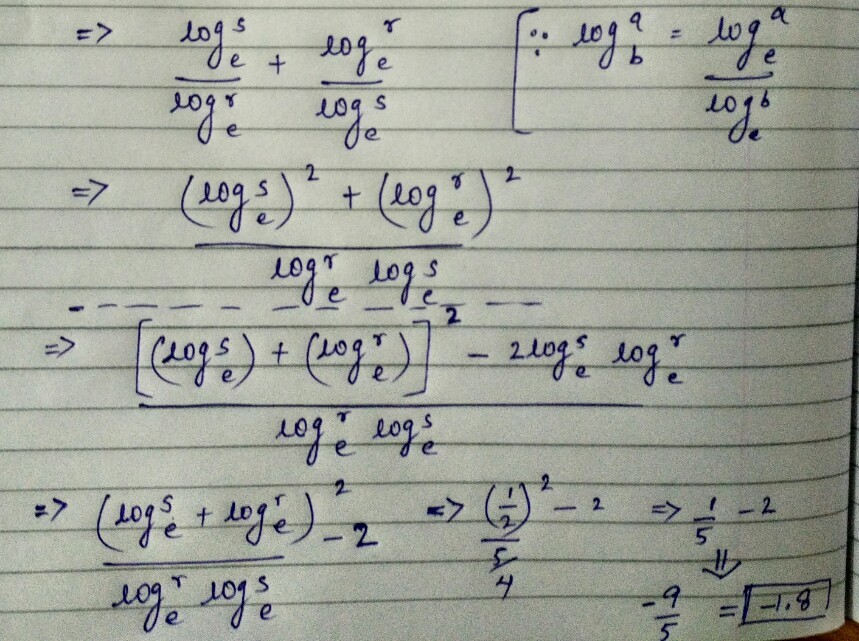Logarithm of imaginary numbers?
If ln r and ln s are the roots of the equation 4 x 2 − 2 x + 5 = 0 ,find the value of lo g r s + lo g s r .
The answer is -1.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
By the quadratic formula the roots of the given equation are
x = 2 ∗ 4 2 ± ( − 2 ) 2 − 4 ∗ 4 ∗ 5 = 4 1 ± i ∗ 1 9 .
Without loss of generality we can assign ln ( r ) and ln ( s ) as the positive and negative roots, respectively.
Now by the change-of-base rule we have that
lo g r ( s ) + lo g s ( r ) = ln ( r ) ln ( s ) + ln ( s ) ln ( r ) .
Next, we find that
ln ( s ) ln ( r ) = 1 − i ∗ 1 9 1 + i ∗ 1 9 × 1 + i ∗ 1 9 1 + i ∗ 1 9 = 2 0 1 − 1 9 + i ∗ 2 1 9 = 1 0 − 9 + i ∗ 1 9 ,
and so
ln ( s ) ln ( r ) + ln ( r ) ln ( s ) = 1 0 − 9 + i ∗ 1 9 + − 9 + i ∗ 1 9 1 0 = 1 0 ∗ ( − 9 + i ∗ 1 9 ) 8 1 − 1 9 − i ∗ 1 8 1 9 =
1 0 ∗ ( − 9 + i ∗ 1 9 ) 1 6 2 − i ∗ 1 8 1 9 = 1 0 ∗ ( − 9 + i ∗ 1 9 ) − 1 8 ∗ ( − 9 + i ∗ 1 9 ) = − 1 0 1 8 = − 1 . 8 .
We can write ln ( r ) ln ( s ) + ln ( s ) ln ( r ) as ln ( r ) ln ( s ) ( ln ( s ) + ln ( r ) ) 2 − 2 ln ( r ) ln ( s ) , and than find its value without computing the actual roots, by Vieta's formulas.
Log in to reply
Yes, I realized that after seeing Raj's solution, (which was posted just a short time after mine).
Let l n r = a and l n s = b . This means l o g r s + l o g s r = l n r l n s + l n r l n s = b a + a b = a b a 2 + b 2 = a b ( a + b ) 2 − 2 a b = 4 5 ( 2 1 ) 2 − 2 ⋅ 4 5 = − 1 . 8