Logarithmic Equation
Given that
lo g 2 ( lo g 8 x ) = lo g 8 ( lo g 2 x ) ,
find the value of ( lo g 2 x ) 2 .
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
lo g 2 ( lo g 8 x ) = lo g 8 ( lo g 2 x )
⟹ lo g 2 ( 3 lo g 2 x ) = 3 lo g 2 ( lo g 2 x )
⟹ lo g 2 ( 3 lo g 2 x ) = lo g 2 ( ( lo g 2 x ) 1 / 3 )
⟹ 3 lo g 2 x = ( lo g 2 x ) 1 / 3
⟹ 2 7 ( lo g 2 x ) 3 = lo g 2 x
⟹ ( lo g 2 x ) 2 = 2 7 .
I understand your method right down to the second last line . From there you are multiplying the RHS by 27 and, after that, diving both sides by Log x to base 2 (?)
Log in to reply
Cross multiplication. lo g 2 x ( lo g 2 x ) 3 = 2 7
l o g 2 ( 3 1 l o g 2 x ) = 3 1 l o g 2 ( l o g 2 x )
3 l o g 2 3 1 + 3 l o g 2 ( l o g 2 x ) = l o g 2 ( l o g 2 x )
2 l o g 2 ( l o g 2 x ) = l o g 2 2 7
l o g 2 x 2 = 2 l o g 2 2 7
l o g 2 x 2 = 2 7
I can see why some find this somewhat tricky at first.
log((1/3) log(x)) = 1/3 log(log(x))
(1/3)*log(x) = (log(x))^(1/3)
(log(x))^3 = 27 (log(x))
(log(x))^2 = 27
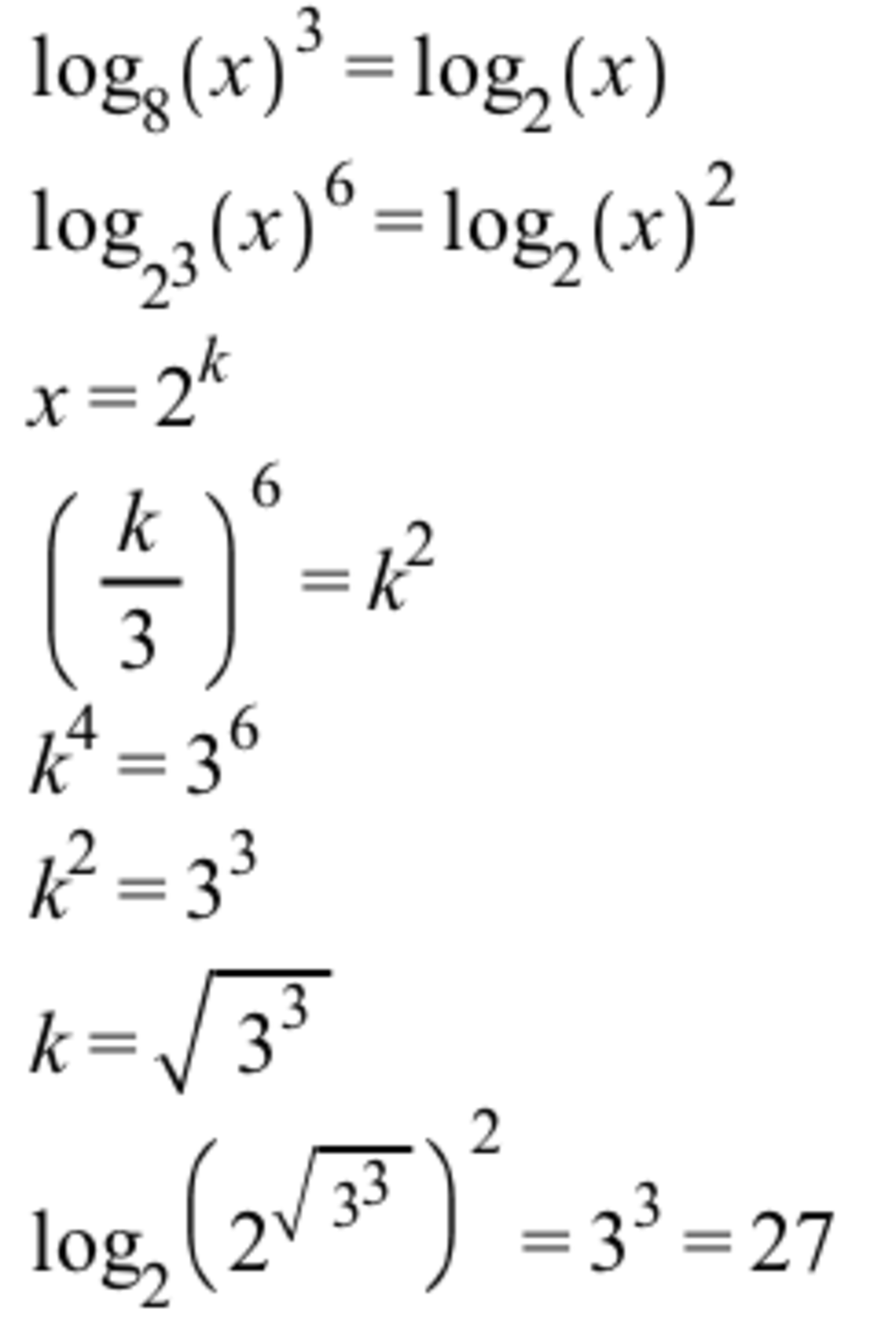
Using the Properties of Logarithms , this equation can be written as
lo g 2 ( ( 3 1 ) lo g 2 x ) = ( 3 1 ) lo g 2 ( lo g 2 x )
⟹ ( 3 1 ) lo g 2 x = ( lo g 2 x ) 3 1
⟹ ( lo g 2 x ) 3 2 = 3 ⟹ lo g 2 x = 3 3 ,
the square of which is 9 ⋅ 3 = 2 7 .