Logarithmic Probability

We can find the solution to this problem if we identify important "turning points" in the expression $\big\lfloor \log _{2}\frac{1}{x}\big\rfloor$ for specific values of x.

$x = 1$ : $\log _{2}(\frac{1}{1}) = \log _{2}1 = 0$

$x = \frac{1}{2}$ : $\log _{2}(\frac{1}{\frac{1}{2}}) = \log _{2}2 = 1$

$x = \frac{1}{4}$ : $\log _{2}(\frac{1}{\frac{1}{4}}) = \log _{2}4 = 2$

$x = \frac{1}{8}$ : $\log _{2}(\frac{1}{\frac{1}{8}}) = \log _{2}8 = 3$

$x = \frac{1}{16}$ : $\log _{2}(\frac{1}{\frac{1}{16}}) = \log _{2}16 = 4$

$x = \frac{1}{32}$ : $\log _{2}(\frac{1}{\frac{1}{32}}) = \log _{2}32 = 5$

$...$

So, for values of $x$ where $1 \geq x > \frac{1}{2}$ , $\big\lfloor \log _{2}\frac{1}{x}\big\rfloor = 0$ , which is even.

For values of $x$ where $\frac{1}{2} \geq x > \frac{1}{4}$ , $\big\lfloor \log _{2}\frac{1}{x}\big\rfloor = 1$ , which is odd.

For values of $x$ where $\frac{1}{4} \geq x > \frac{1}{8}$ , $\big\lfloor \log _{2}\frac{1}{x}\big\rfloor = 2$ , which is even.

For values of $x$ where $\frac{1}{8} \geq x > \frac{1}{16}$ , $\big\lfloor \log _{2}\frac{1}{x}\big\rfloor = 3$ , which is odd.

For values of $x$ where $\frac{1}{16} \geq x > \frac{1}{32}$ , $\big\lfloor \log _{2}\frac{1}{x}\big\rfloor = 4$ , which is even.

$...$

Therefore, the values for which $\big\lfloor \log _{2}\frac{1}{x}\big\rfloor$ is even is $\frac{1}{2} + \frac{1}{8} + \frac{1}{32} ... = \displaystyle\sum_{n=1}^{\infty} \frac{1}{2^{2n - 1}} = \displaystyle\sum_{n=1}^{\infty} \frac{2}{4^{n}}$

The values for which for which $\big\lfloor \log _{2}\frac{1}{x}\big\rfloor$ is odd is $\frac{1}{4} + \frac{1}{16} + \frac{1}{64} ... = \displaystyle\sum_{n=1}^{\infty} \frac{1}{2^{2n}} = \displaystyle\sum_{n=1}^{\infty} \frac{1}{4^{n}}$

We can evaluate the infinite sum for which $\big\lfloor \log _{2}\frac{1}{x}\big\rfloor$ is odd by using the formula $(a) + (a \times r) + (a \times r^{2}) + (a \times r^{3})... = \frac{a}{1 - r}$ (as a side note, this formula only works when $|r| < 1$ ). The sum for odd numbers can be rewritten as $(\frac{1}{4}) + (\frac{1}{4} \times \frac{1}{4}) + (\frac{1}{4} \times (\frac{1}{4})^{2}) + (\frac{1}{4} \times (\frac{1}{4})^{3})... = \frac{\frac{1}{4}}{1 - \frac{1}{4}} = \frac{\frac{1}{4}}{\frac{3}{4}} = \frac{4}{3 \times 4} = \boldsymbol{\frac{1}{3}}$

Let $f(x) = \lfloor \log_2 \frac 1x \rfloor.$ Then:

• If $x > \tfrac12$ , then $0 \leq \log_2 \frac 1x < 1$ so that $f(x) = 0$ is even.

• If $x \leq \tfrac 12$ , $f(x) = f(2x) + 1$ , so that $f(x)$ has the opposite parity of $f(2x)$ .

Therefore, $\mathbb P (f(x)\ \text{is odd}) = \mathbb P\big(x \leq \tfrac12\ \text{and}\ f(2x)\ \text{is even}\big) = \tfrac12\big(1 - \mathbb P (f(x')\ \text{is odd})\big);$ this is a simple linear equation $P = \tfrac12(1 - P)$ , with solution $P = \mathbb P (f(x)\ \text{is odd}) = \boxed{1/3 \approx 0.333}.$

---

Generalization for arbitrary base $b > 1$ :

If you pick a number $x$ randomly (and uniformly distributed) on $[0,1]$ , the probability that $\lfloor \log_b \frac 1 x \rfloor$ is odd is equal to $P = \frac 1{1 + b}.$ The reasoning is similar: Let $f(x) = \lfloor \log_b \frac 1x \rfloor.$ Then:

• If $x > \tfrac1b$ , then $0 \leq \log_b \frac 1x < 1$ so that $f(x) = 0$ is even.

• If $x \leq \tfrac 1b$ , $f(x) = f(bx) + 1$ , so that $f(x)$ has the opposite parity of $f(bx)$ .

Therefore, $\mathbb P (f(x)\ \text{is odd}) = \mathbb P\big(x \leq \tfrac1b\ \text{and}\ f(bx)\ \text{is even}\big) = \tfrac1b\big(1 - \mathbb P (f(x')\ \text{is odd})\big);$ this is a simple linear equation $P = \tfrac1b(1 - P)$ , or $bP = 1 - P$ , with solution $P = \mathbb P (f(x)\ \text{is odd}) = \frac{1}{1+b}.$

We are looking for the measure of the preimage of the set

$[1,2) \bigcup [3,4) \bigcup [5,6)....$

via $\log_{2}\frac{1}{x}$ . Representing x in binary we must have that

$x \in (0.01_{2},0.1_{2}] \bigcup (0.0001_{2},0.001_{2} ] \bigcup ( 0.000001_{2},0.00001_{2}].....$

Adding the lengths of the intervals we get the probability

$P = 0.01_{2} + 0.0001_{2} + 0.000001_{2} + ... = 0.010101..._{2}$

Now $3P = P + 2P = 0.010101..._{2} + 0.101010..._{2} = 0.111111..._{2} = 1$

So $P=\frac{1}{3}$

Log base 2 of 1/x can be rewritten as -log base 2 of x.

Graphing -log base 2 of x yields segments of length (1 - 1/2) at y=0, segment of (1/2-1/4) at y=1, (1/4-1/8) at y=2, etc.

The function that gives the segment’s length at y=n is given by 2^{-n-1}

The probability of y being odd is the same as the sum of the segments at n being odd;

This turns into the infinite sum of 4^{-n}, 1/4 + 1/16 + 1/64....

which simplifies to 1/3, or 0.333.

Matlab Solution:

q=10000;     %sqrt of number of experiments to perform
r = rand(q);  %gen matrix of rand numbers
r = r(:);         %make into vector for easy processing  
x= floor(log(1./r)./log(2));    %apply function
odd = mod(x,2);    %find odd vals of output
sum(odd)/q^2       %find p

ans = 0.3334

f(x)=floor(lg(1/x))

From 1/2 to 1 the function is 0: even

From 1/4 to 1/2 the function is 1: odd

From 1/8 to 1/4 the function is 2: even

From 1/16 to 1/8 the function is 3: odd etc

Each even interval has a corresponding odd interval which is half as wide, so overall the P(even)=2*P(odd)

P(even) = 2/3

P(odd) = 1/3

The approach which I followed is very naive I guess!

I plotted the graph of the function using maxima,

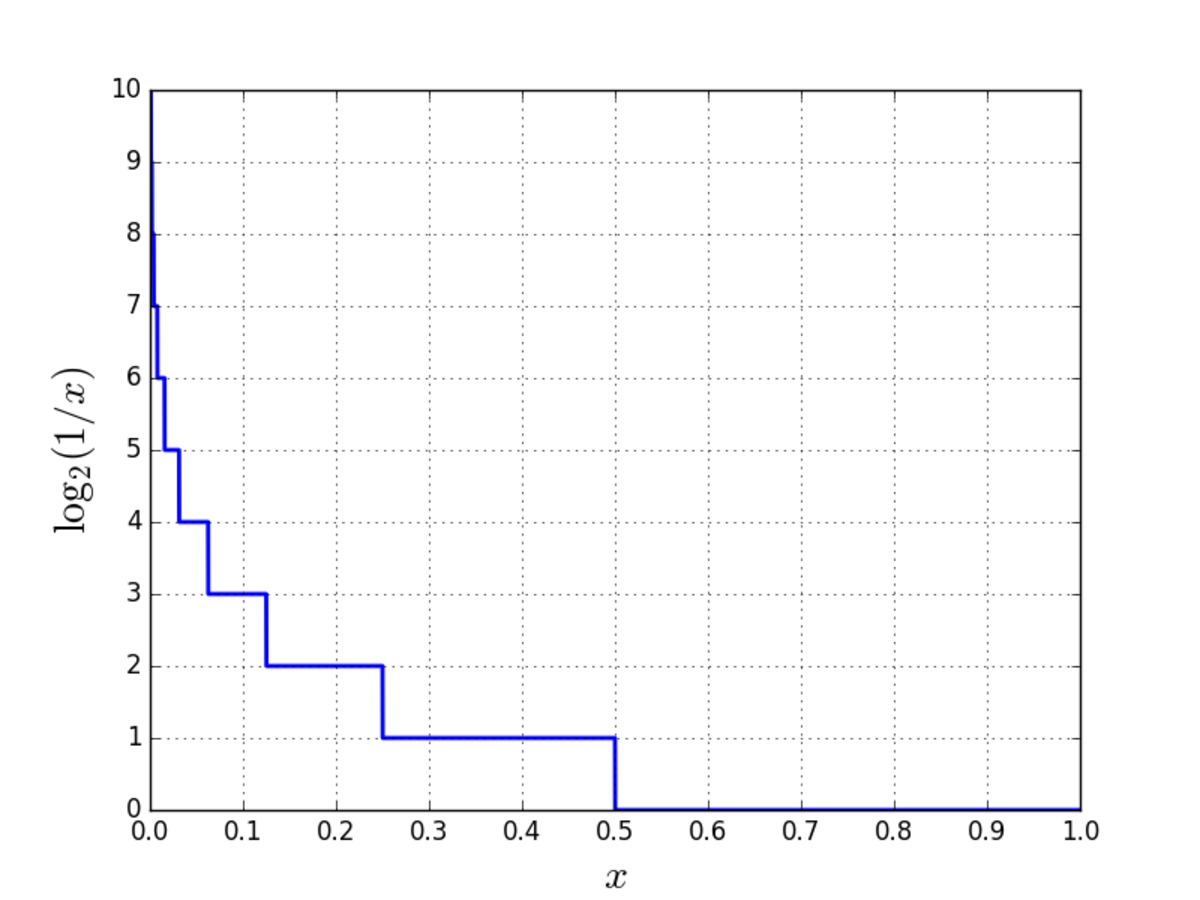
Looking at the plot we can easily come up with this series for the probability of odd number being chosen:

$1/4 + 1/4^2 + 1/4^3 + 1/4^4 + 1/4^5 \dots$ which converges to $1/3$ .

import java.util.*; public class Program{

public static void main(String[] args) {
    double count=0, countodd=0, counteven=0;
    double X;
    for(int counter= 1; counter <=10000000; counter++ ){
    X = Math.random();
    double y = (Math.log(1/X))/(Math.log(2));
    double z = Math.floor(y);
    count= count+1;
    if(z%2==0){
    counteven= counteven+1;

    }
    else{
    countodd=countodd+1;
    }
    }
    System.out.println((countodd/count));
}

}

For the logs, I could only find log base 10, so I used change of base formula. I used mod 2 to find if the integer was even or not.