Never-ending logarithmic series
lo g 2 x + lo g 2 ( x ) + lo g 2 ( x ) + lo g 2 ( x ) + … = 4
What is the positive value of x that satisfies the equation above?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Discussions for this problem are now closed
thank you sir. You're right. One term has been left by mistake. I am making it done. Nice solution.. @brian charlesworth
Following logarithmic laws: Log(x)^k = klog(x) .You are using a square root on each term which. This means that each term goes up to the power of a half from the last one so log2(x) + log2(x)^1/2 ....=4 so using the sum to infinity equation: Sn= a(1-r^n)/ 1-r where a = the first term (log2(x)) and r= 1/2 then it becomes 2= log2(x) and then 2^2 =x which is 4!
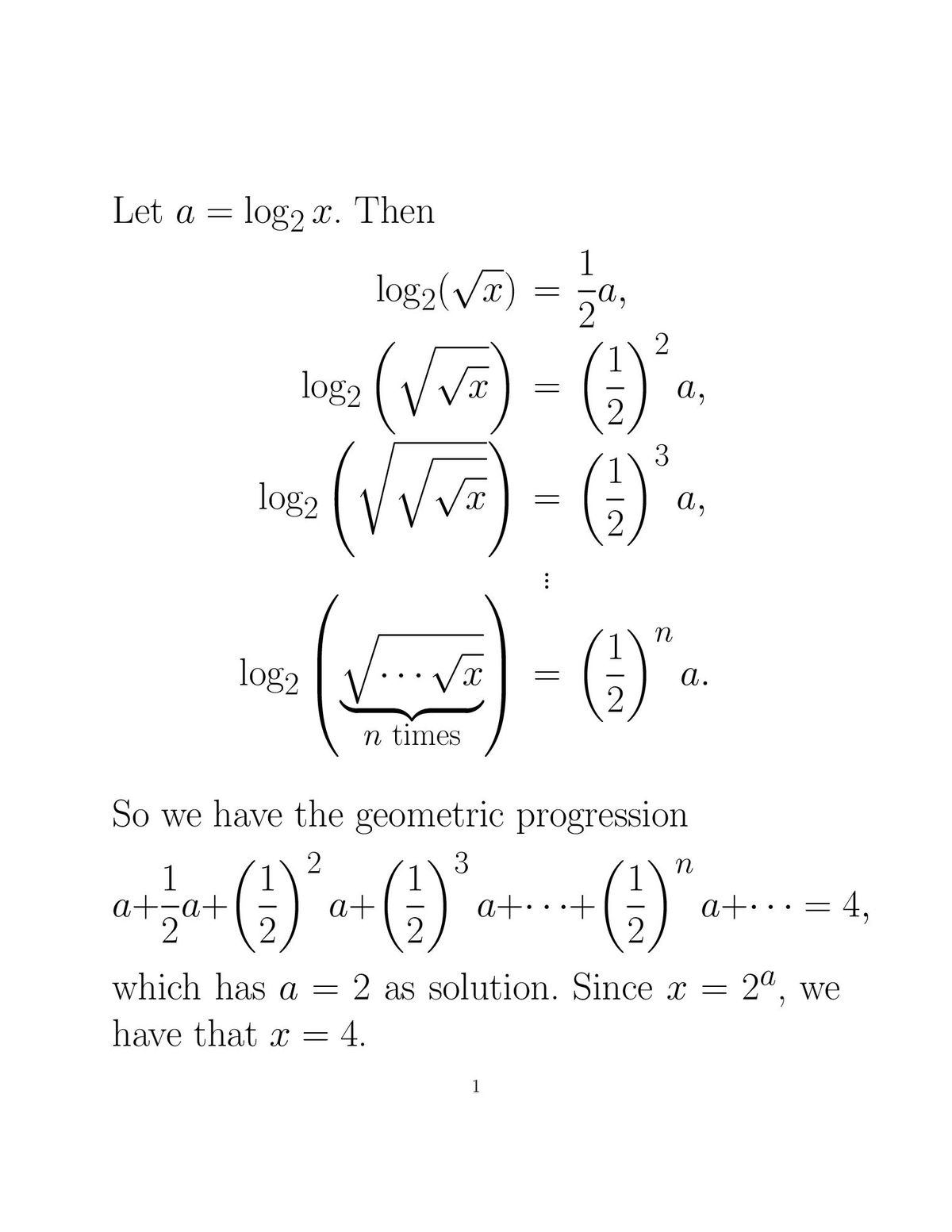
Assuming that there should also be the term lo g 2 ( x ) after lo g 2 ( x ) then the equation becomes
lo g 2 ( x ) + lo g 2 ( x 2 1 ) + lo g 2 ( x 4 1 ) + lo g 2 ( x 8 1 ) + . . . . . . = 4
⟹ ( 1 + 2 1 + 4 1 + 8 1 + . . . . . . . ) ∗ lo g 2 ( x ) = 4
⟹ 2 ∗ lo g 2 ( x ) = 4 ⟹ lo g 2 ( x ) = 2 ⟹ x = 2 2 = 4 .
@Sandeep Bhardwaj Nice question, but I think you have omitted a term in the equation; please see my note above.