Logarithmic spiral

Calculus Level 3

A particle moves along a spiral so that its path is given by r ⃗ ( t ) = e − α t ( cos ⁡ ( t ) sin ⁡ ( t ) ) , t ∈ [ 0 , ∞ ) \vec r(t) = e^{-\alpha t} \left( \begin{array}{c} \cos(t) \\ \sin(t) \end{array} \right), \quad t \in [0,\infty) with the time t t and a decay constant α = 0.1 \alpha = 0.1 . What is the total distance of the path from r ⃗ ( 0 ) = ( 1 , 0 ) \vec r(0) = (1,0) to r ⃗ ( ∞ ) = ( 0 , 0 ) \vec r(\infty) = (0,0) , that is covered by the particle for all time?


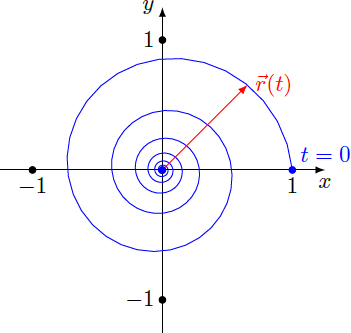
The answer is 10.05.

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Markus Michelmann
Sep 24, 2017

The velocity of the particle is given by v ⃗ ( t ) = r ⃗ ˙ ( t ) = − α e − α t ( cos ⁡ ( t ) sin ⁡ ( t ) ) ⏟ e ⃗ r ( t ) + e − α t ( − sin ⁡ ( t ) cos ⁡ ( t ) ) ⏟ e ⃗ ϕ ( t ) = e − α t ( e ⃗ ϕ ( t ) − α e ⃗ r ( t ) ) \vec v(t) = \dot{\vec{r}} (t) = - \alpha e^{-\alpha t} \underbrace{\left( \begin{array}{c} \cos(t) \\ \sin(t) \end{array} \right)}_{\vec e_r(t)} + e^{-\alpha t} \underbrace{\left( \begin{array}{c} -\sin(t) \\ \cos(t) \end{array} \right) }_{\vec e_\phi(t)} = e^{-\alpha t} (\vec e_\phi(t) - \alpha \vec e_r(t)) with ∣ e ⃗ r ∣ = ∣ e ⃗ ϕ ∣ = 1 |\vec e_r| = |\vec e_\phi| = 1 and e ⃗ r ⋅ e ⃗ ϕ = 0 \vec e_r \cdot \vec e_\phi = 0 . Therefore, the absolute value of the velocity results to v ( t ) = ∣ v ⃗ ( t ) ∣ = v ⃗ ( t ) ⋅ v ⃗ ( t ) = 1 + α 2 ⋅ e − α t v(t) = |\vec v(t)| = \sqrt{\vec v(t) \cdot \vec v(t)} = \sqrt{1 + \alpha^2} \cdot e^{-\alpha t} By integrating the velocity over time, the path length is obtained: s = ∫ 0 ∞ v ( t ) d t = 1 + α 2 ∫ 0 ∞ e − α t d t = 1 + α 2 α ≈ 10.05 s = \int_0^\infty v(t) dt = \sqrt{1 + \alpha^2} \int_0^\infty e^{-\alpha t} dt = \frac{\sqrt{1 + \alpha^2}}{\alpha} \approx 10.05

4 Helpful 0 Interesting 0 Brilliant 0 Confused

We can actually do it directly without calculating the velocity , but that solution is more lengthy than yours . For a function y = f ( x ) y=f(x)

s = ∫ a b 1 + ( y ′ ) 2 d x s = \int_{a}^{b} \sqrt{1+\left(y^{'}\right)^2 } dx

Sabhrant Sachan - 3 years, 8 months ago

Log in to reply

In princple, you're right. I just thought it would be more obvious from a physical point of view to speak of a velocity. Furthermore, the spiral can not be uniquely represented by a function y = f ( x ) y = f(x) , since several (or even infinite) y y values ​​are associated with an x x -value.

Markus Michelmann - 3 years, 8 months ago

Log in to reply

you are absolutely correct , we cannot uniquely represent it as y = f ( x ) y=f(x) that is why we will integrate it in the parametric form .

d y = ( − α e − α t sin ⁡ t + e − α t cos ⁡ t ) d t d x = ( − α e − α t cos ⁡ t − e − α t sin ⁡ t ) d t dy = \left( -\alpha e^{-\alpha t} \sin{t} + e^{-\alpha t} \cos{t} \right) dt \\ dx = \left( -\alpha e^{-\alpha t} \cos{t} - e^{-\alpha t} \sin{t} \right) dt

The end result is the integral s = 1 + α 2 ∫ 0 ∞ e − α t d t s = \sqrt{1+\alpha^2} \int_{0}^{\infty} e^{-\alpha t} dt

Sabhrant Sachan - 3 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...