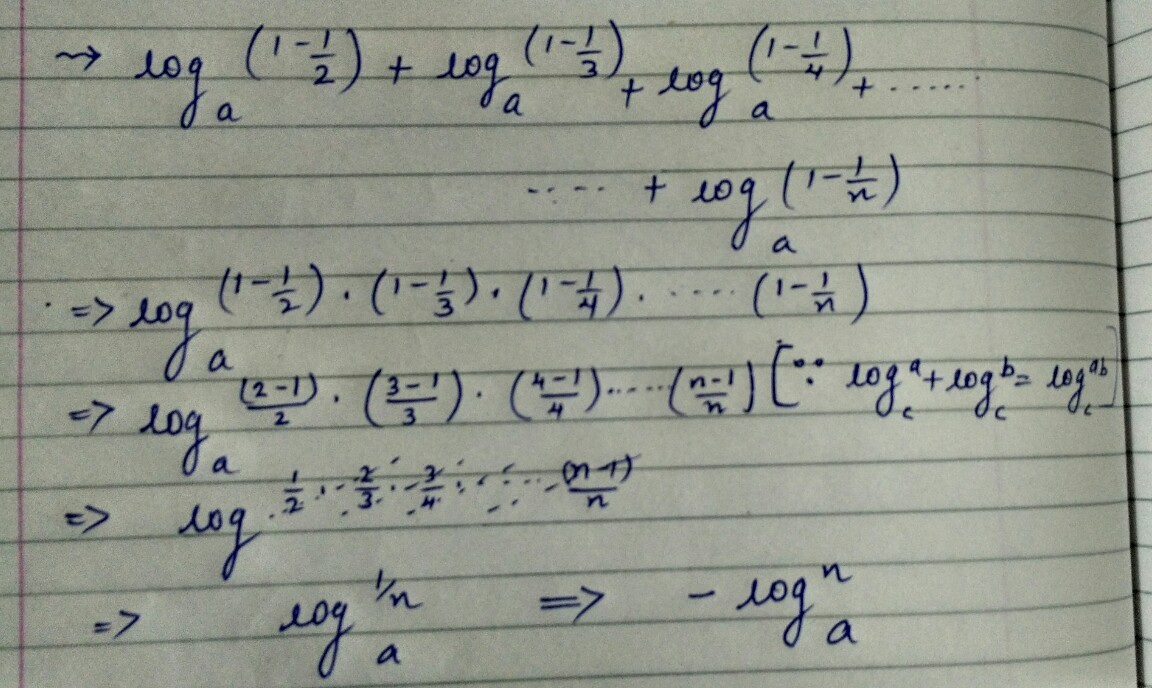Logarithms' challenger #2

Algebra Level 3

$\text{Find the value of:}$ $\log_ {a}{\left(1-\frac{1}{2}\right)}+\log_ {a}{\left(1-\frac{1}{3}\right)}+\log_ {a}{\left(1-\frac{1}{4}\right)}...+\log_ {a}{\left(1-\frac{1}{n}\right)}$

This problem is a part of this set .

-\log_{a}{n}

\frac{1}{n}

1 None of these.

n-1

\log_{a}{n}

4 solutions

Raj Rajput
Oct 10, 2015

Sai Aryanreddy
Oct 11, 2015

If anyone found the above screenshots unclear, here is the answer in TeX form:

$\log_a(1-\frac{1}{2})+\log_a(1-\frac{1}{3})+\log_a(1-\frac{1}{4})+...\log_a(1-\frac{1}{n})$

Reducing the terms inside the logarithms such as $1-\frac{1}{2}=\frac{1}{2}$ and then combining the logarithms gives:

= $\log_a((\frac{1}{2}*\frac{2}{3}*\frac{3}{4}*....*\frac{n-2}{n-1}*\frac{n-1}{n})$

The numerator and denominator of each fraction will cancel leaving only the 1/n term:

= $\log_a(1/n)=log_a(n^{-1})$ , which can be rewritten as $-\log_a(n)$

Scott Ripperda - 5 years, 8 months ago

Atul Shivam
Oct 17, 2015

Using the property of log ie. $log(a)+log(b)= log(ab)$ this can be reduced to $-log(n)$ with base a

Ramiel To-ong
Oct 12, 2015

using mathematical induction,

Logarithms' challenger #2

4 solutions

0 pending reports