Logging The Summation!!
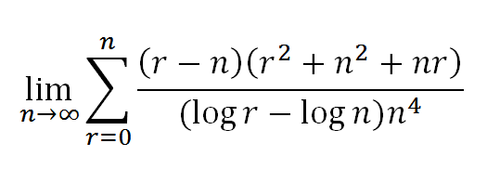 Evaluate to 4 decimal places:
Note if your answer comes in a natural logarithm give the answer as the logarithm with base 10;e.g if your answer is
then give
as answer
Evaluate to 4 decimal places:
Note if your answer comes in a natural logarithm give the answer as the logarithm with base 10;e.g if your answer is
then give
as answer
The answer is 0.6020.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A Quick Solution: ( lo g r − lo g n ) n 4 ( r − n ) ( r 2 + n 2 + n r ) = n 4 lo g ( n r ) r 3 − n 3 = lo g n r n 3 r 3 − 1 n 1
Now using Riemann Sums: = ∫ 0 1 lo g x x 3 − 1 d x
This is a standard integral which can be solved by differentiating through the integral, the answer comes out to be: ln ( 4 ) According to the condition given the answer to be submitted is: lo g 4 ≈ 0 . 6 0 2 0