LOGging X

$\log _{ 3 }{ \left( \log _{ 2 }{ \left( \log _{ 3 }{ x } \right) } \right) } = 0$

$\implies \quad { 3 }^{ 0 } = \log _{ 2 }{ \left( \log _{ 3 }{ x } \right) }$

$\implies \quad { 2 }^{ 1 } = \log _{ 3 }{ x }$

$\implies \quad x = { 3 }^{ 2 } =\boxed{ \large{ 9}}$

$\log_3 (\log_2(\log_3 (x)) = 0$ $\implies \log_3 (\log_2(\log_3 (x)) = \log_3 (1)$ $\implies \log_2 (\log_3 (x)) = 1$ $\implies \log_2 (\log_3 (x)) = \log_2 (2)$ $\implies \log_3 (x) = 2$ $\implies x = 3^{2} \implies x = 9$

Therefore, $x$ equals $\boxed {9}$

first, change the first logarithm with a base of 3 into exponential form. The result will be like this. 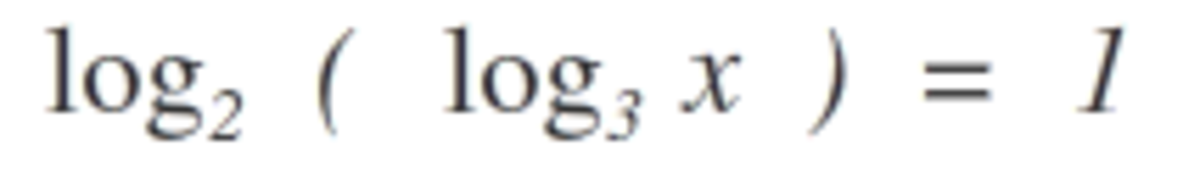then, do the same process to second logarithm. and it will be like this. 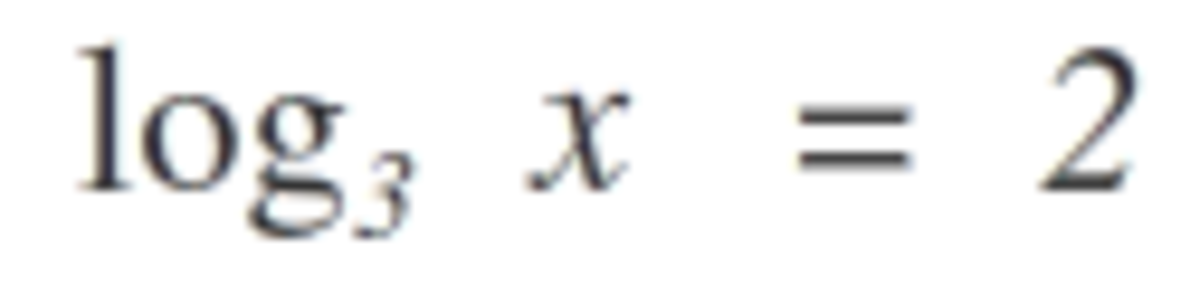with that, you can now get the value of x by changing it into exponential form again and came up with the answer x = 9.