Logic Gate from Switches

Electricity and Magnetism Level 2

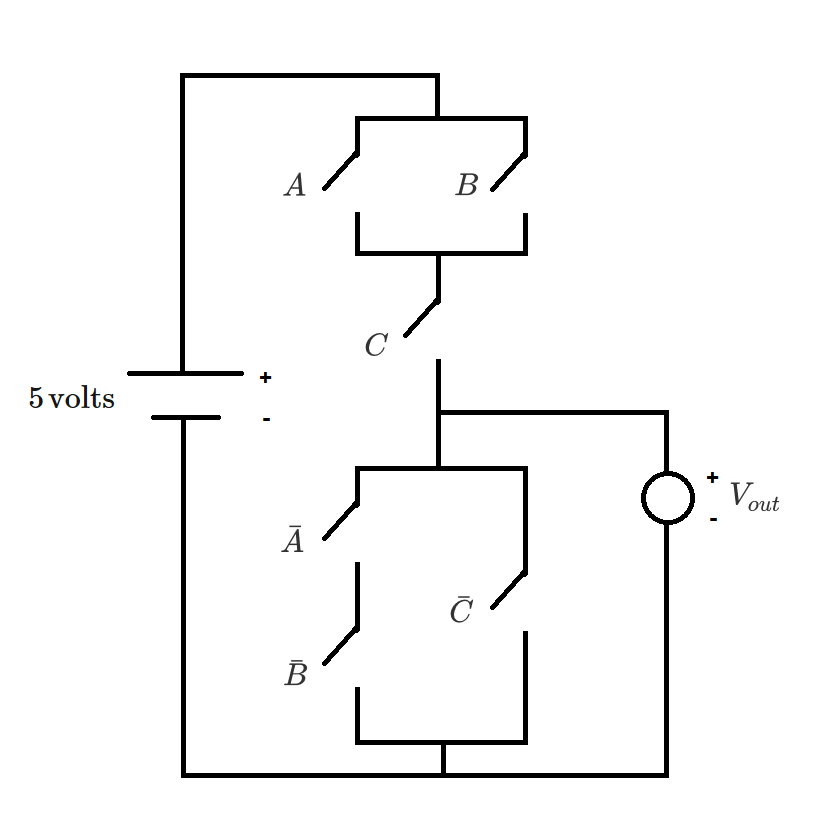
The diagram above shows a logic gate with Boolean logical inputs $A, B, C$ in the top half, and their logical negations $\bar{A}, \bar{B}, \bar{C}$ in the bottom half. The source voltage is 5 volts.

$V_{out} = 5$ corresponds to a high (true) logical output, and $V_{out} = 0$ corresponds to a low (false) logical output. A switch is closed (conducting) if the associated logical signal is high (true), and the switch is open (non-conducting) if the associated logical signal is low (false).

Which logical operation does this gate perform?

Note: In Boolean algebra, the AND operation is specified by logical inputs multiplied together. The OR operation is specified by logical inputs added together. For example, (A AND B) is specified by $AB$ , and (A OR B) is specified by $A + B$ .

\large{\bar{A} \bar{B} + \bar{C}}

\large{(A + B) C}

\large{A B + C}

\large{(A + B) C + \bar{A} \bar{B} + \bar{C} }

1 solution

Joseph Newton
Mar 15, 2018

No matter which path the current takes through the wires, it must always pass through $C$ , so we can immediately conclude that $C$ must be true and therefore $\bar{C}$ must be false regardless of $A$ and $B$ . To get to $C$ , the current can either pass through $A$ or $B$ .

Whether $A$ is true , $B$ is true or both $A$ and $B$ are true , the $\bar{C}$ switch is always false and at least one of $\bar{A}$ or $\bar{B}$ is false , so the current cannot pass through any of $\bar{A}$ , $\bar{B}$ or $\bar{C}$ and must pass through $V_{out}$ . From this we can conclude that $C$ is true and either $A$ or $B$ or both is true.

This equates to the logical operation C AND (A OR B), which algebraically is $(A+B)C$

Logic Gate from Switches

1 solution

0 pending reports