Logic puzzle 4
There are 25 horses and you have to determine the 3 fastest horses. You don't have a stopwatch so you can't measure the time and you can race only a maximum of 5 horses in a single race. How many minimum number of races would you need to get the result?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
name the horses as H1, H2... H25 and arrange them in 5 rows :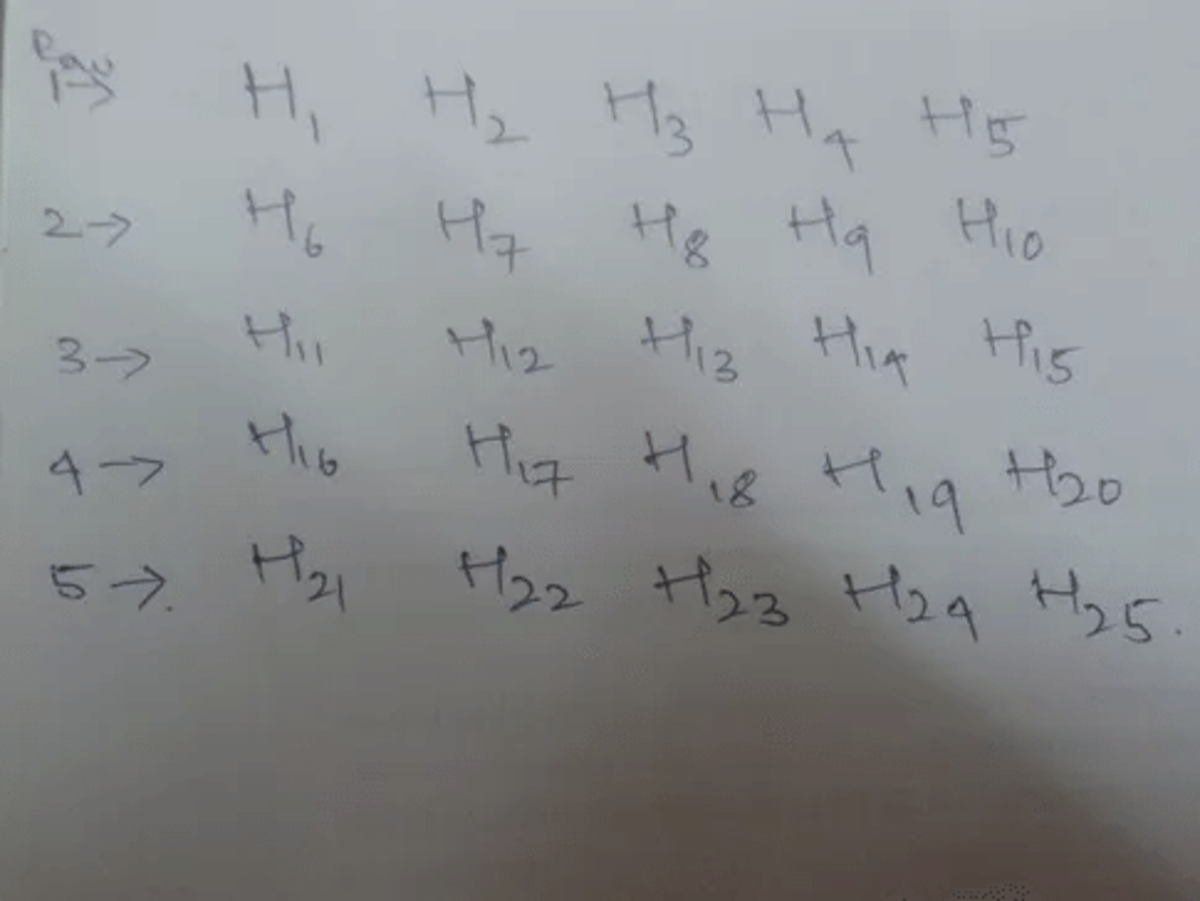
Now you race the 5 horses in each row and note down the 3 fastest horses in each race. Now that makes it 5 races.
Now assume the 3 fastest horses of the first race are H1, H2 and H3 and similarly H6, H7 and H8 of the second race and so on.
From this it is clear that horses H4 and H5 who finished fourth and fifth in the race can not be the fastest 3 of the lot and hence can be eliminated. Similarly all the other horses that finished fourth and fifth in the other four races can be eliminated.
Now have another race among all the horses that finished first in their respective races ( H1, H6, H11, H16, H21 ) and note down the 3 fastest. Assume H1, H6 and H11 are the 3 fastest.
Now H16 and H21 and all the horses in their rows can be eliminated since H16 and H21 finished 4th and 5th and they are the winners of their respective races and thus the other horses in row 4 and row 5 can not finish in the top 3.
Now H11 finished 3rd in the race between the group toppers and since H12 andH13 are slower than H11 they can be eliminated.
H6 finished 2nd in the race between the group toppers and the only horse that could possibly finish 3rd in that row is H7, so H8 can be eliminated as it is slower than H7.
H1 is the fastest in both the races so it is safe to say that H1 is the fastest among all 25 horses and H1 can be eliminated.
So now we are left with only 5 horses - H2, H3 H6, H7 and H11 and a race between these 5 horses will determine the 2nd and 3rd fastest among the 25 horses. Assume H2 and H3 finish first and second in this race. H6, H7 and H11 can be eliminated.
So H1 , H2 and H3 are the 3 fastest horses
And the minimum number of races required to determine this is 7.