Logical Logarithms
b − c lo g a = c − a lo g b = a − b lo g c
a , b , c are distinct positive real numbers that satisfy the above equation. What is
a a × b b × c c = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Assume b − c lo g a = c − a lo g b = a − b lo g c = k ( k ∈ ℜ )
Then,
lo g a = k ⋅ b − k ⋅ c ⟹ a lo g a = k ( a ⋅ b − a ⋅ c )
⟹ lo g a a = k ( a ⋅ b − a ⋅ c )
Similarly, lo g b b = k ( c ⋅ b − a ⋅ b ) , lo g c c = k ( a ⋅ c − b ⋅ c )
Therefore,by adding the above results,
lo g ( a a ⋅ b b ⋅ c c ) = k ( a ⋅ b − a ⋅ c ) + k ( c ⋅ b − a ⋅ b ) + k ( a ⋅ c − b ⋅ c ) = 0
Hence, a a ⋅ b b ⋅ c c = 1
Upvoted !!! ⌣ ¨
Good job... :)
I have used a cheat code to solve this question. Since we are equating three terms, we can assume that these three expressions have limits when all a, b, c are almost equal (i.e., c -> a and b -> a). But in that case, the denominator would be too small. In order for the expression to have a limit, the numerator should also be infinitesimally small. In other words, the expression should be in 0/0 form.
This is possible only if log a = 0 or a = 1. Since a,b,c are almost equal, we can write a=b=c=1
Therefore a^a * b^b * c^c = 1^1 1^1 1^1 = 1 Therefore the answer is 1
Moderator note:
This solution has been marked wrong. we cannot make the assumption that "these three expressions have limits when all a, b, c are almost equal" simply because we are equating three terms.
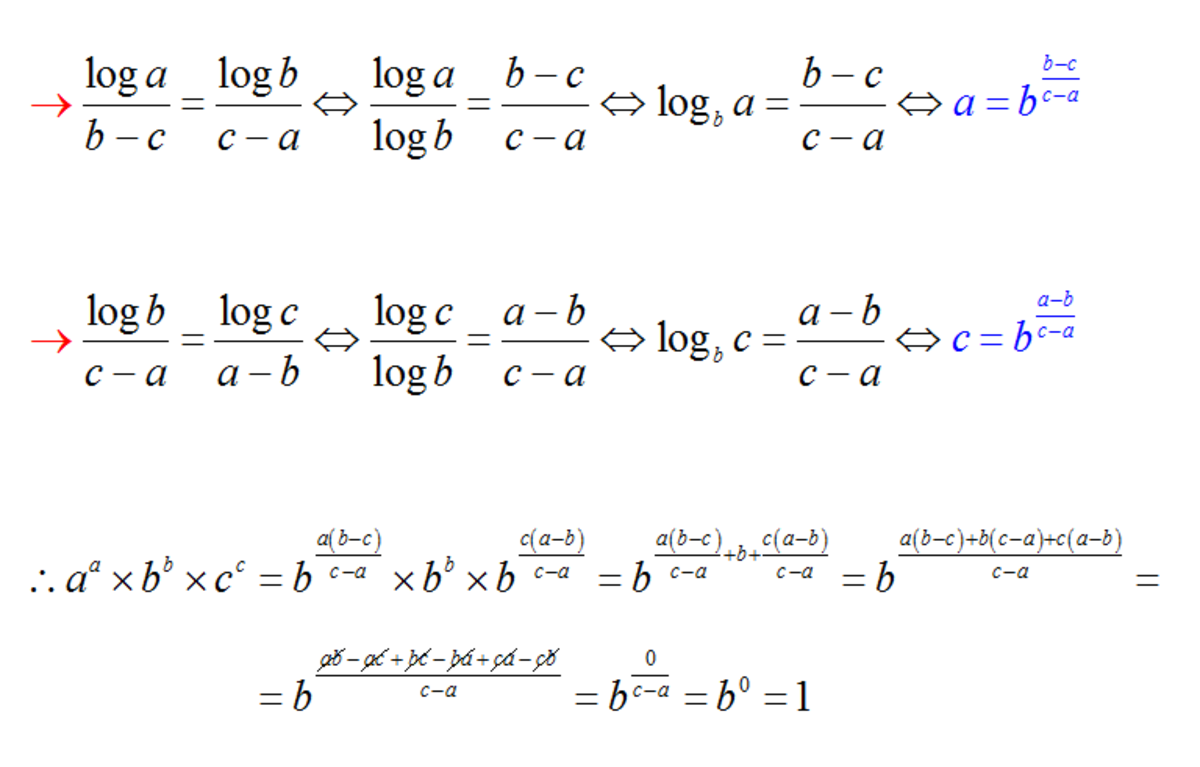
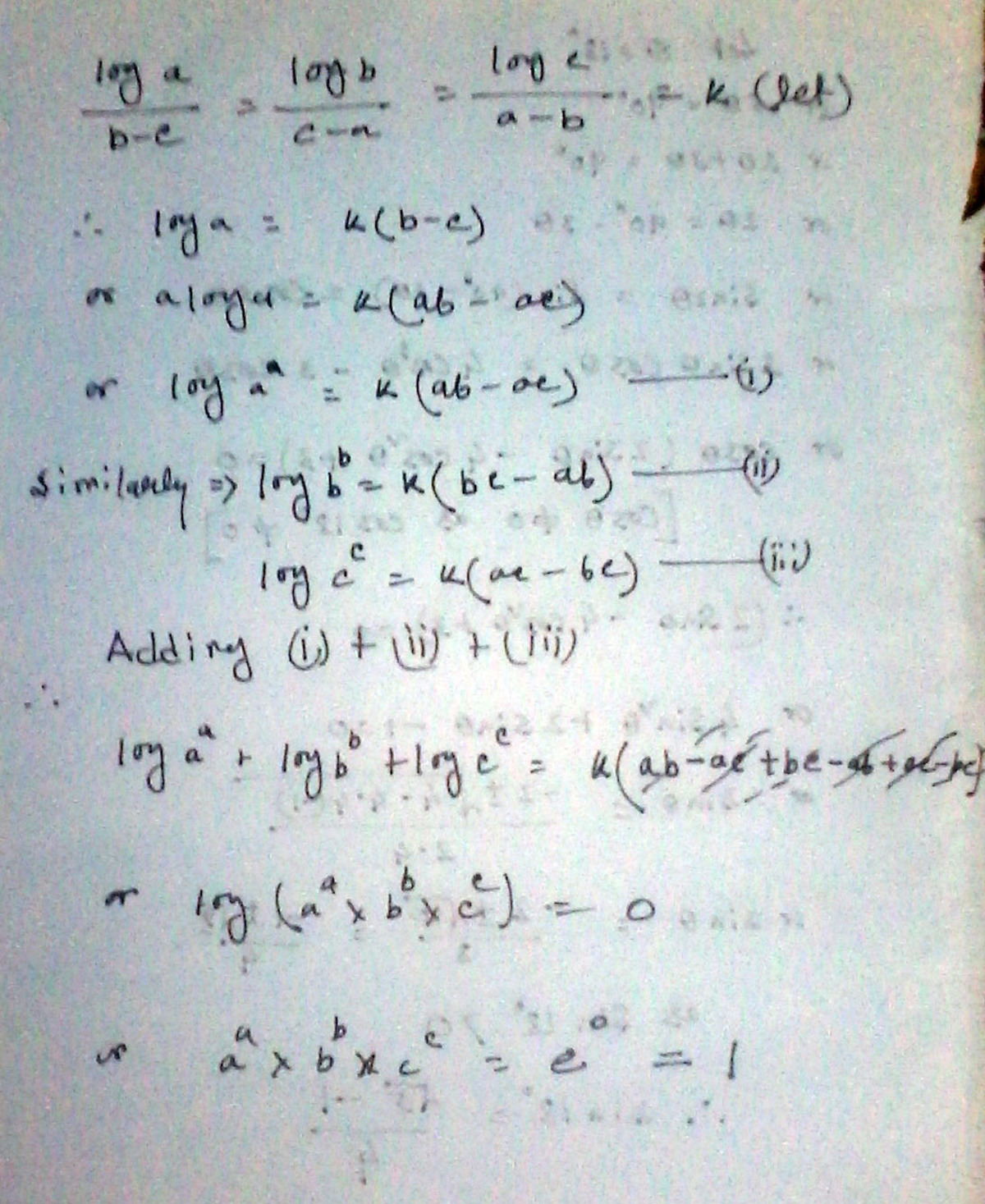
log a = m (b - c)
log b = m(c - a)
log c = m(a - b)
log (a^a)(b^b)(c^c) = a log a + b log b + c log c =
a m (b - c) + b m (c - a) + c m (a - b) = 0
Then
(a^a)(b^b)(c^c) = 1