Logs (but not the mathematical kind)
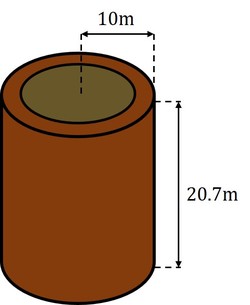 Consider a cylindrical log of height
and radius
as shown.
Consider a cylindrical log of height
and radius
as shown.
What width of bark is necessary for of the volume of the log to be its bark?
Note : No units needed!
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the log is uniform, we can immediately ignore the height of the log and focus on its cross section only.
Let x represent the radius of the non-bark component of the log. This yields the following diagram.
The area of the non-bark component of the log is given by π × x 2 , while the area of the area of the total log is given by π × 1 0 2 = 1 0 0 π . We can combine these to a single equation: 1 0 0 π π × x 2 = 4 1 . (Note: we get 4 1 from the area of the whole log - the area of the bark: 1 − 4 3 = 4 1 ).
π is present in both the numerator and denminator so cancels, and further simplification yields 4 x 2 = 1 0 0 .
x 2 = 2 5
x = 2 5 = 5 (we take the positive root only since the question concerns length).
This shows that the radius of the non-bark component is 5 . We can then find the width of the bark by minusing this from the total log radius, yielding 1 0 − 5 = 5 . So the solution is 5 .
Alternatively, you could solve the problem with scale factors. A S F = L S F 2 , and 4 1 = 2 1 . 1 0 − 2 1 × 1 0 = 5 .