Logs of Logs

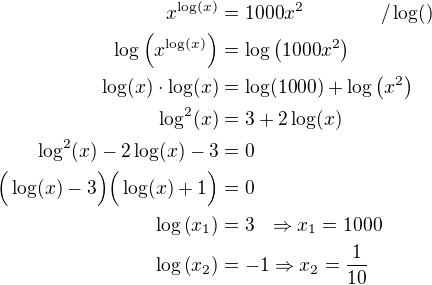
Assuming that $\log$ is the common log, i.e., base 10, take log of both sides to get

$\log(x)*\log(x) = \log(1000) + 2\log(x) = 3 + 2\log(x)$ .

Letting $a = \log(x)$ the equation becomes

$a^{2} - 2a - 3 = 0 \Longrightarrow (a - 3)(a + 1) = 0.$

So the solutions are

$a = \log(x) = 3 \Longrightarrow x = 10^{3} = 1000$ and

$a = \log(x) = -1 \Longrightarrow x = 10^{-1} = \frac{1}{10}.$

Now as we are looking for an integer, after confirming that $x = 1000$ does indeed satisfy the original equation we can conclude that the answer is $x = \boxed{1000}$ .

There must be two solutions. x = 1000 and 0.1

By observation, substitution and calculation with most possible trials, n =1000.