Lonely Quartic Rational Root

Algebra Level 4

Prove that $f(x) = 10x^4 + 43x^3 - 68x^2 - 5x +33$ has exactly one rational root $\alpha$ . Fnd $100 \alpha$ .

The answer is -550.

2 solutions

Chew-Seong Cheong
Sep 21, 2016

According to the rational root theorem , the possible rational roots are: $\pm 1, \pm 3, \pm 11, \pm 33, \pm \frac 12, \pm \frac 32, \pm \frac {11}2, \pm \frac {33}2, \pm \frac 15, \pm \frac 35, \pm \frac {11}5, \pm \frac {33}5, \pm \frac 1{10}, \pm \frac 3{10}, \pm \frac {11}{10}, \pm \frac {33}{10}$

And the respective values of $f(x)$ are as follows.

$\begin{array} {rrrrrrrr} x & f(x) & x & f(x) & x & f(x) & x & f(x) \\ \hline 1 & 13 & 0.5 & 19.5 & 0.2 & 29.64 & 0.1 & 31.864 \\ 3 & 1377 & 1.5 & 68.25 & 0.6 & 16.104 & 0.3 & 26.622 \\ 11 & 195393 & 5.5 & 14253.25 & 2.2 & 385 & 1.1 & 17.094 \\ 33 & 13330317 & 16.5 & 915799.5 & 6.6 & 28374.984 & 3.3 & 2007.192 \\ -1 & -63 & -0.5 & 13.75 & -0.2 & 30.952 & -0.1 & 32.778 \\ -3 & -915 & -1.5 & -207 & -0.6 & 3.528 & -0.3 & 27.3 \\ -11 & 81037 & \color{#D61F06}{-5.5} & \color{#D61F06}{0} & -2.2 & -508.728 & -1.1 & -86.372 \\ -33 & 10240065 & -16.5 & 529641.75 & -6.6 & 3716.328 & -3.3 & -1050.39 \end{array}$

There is only one root $\alpha = -5.5$ . Therefore, $100 \alpha = \boxed{-550}$ .

Sir, is this the only standard method of computing the roots of any polynomial with degree, $n > 2$ ?

What happens when $n$ gets very large? Also,what if there are a lot of divisors of both the leading coefficient and the constant term of the polynomial? I don't think anyone would have such patience to use Rational Root theorem and put each number one by one without any computational aid.

I would like to know what other ways are possible to solve problems like these.

Tapas Mazumdar - 4 years, 8 months ago

Actually I am using a spreadsheet it is very fast. Only presentation takes time. There is a method presented by Frank who set the problem. But I don't quite understand it. You can look up G-filtered Polycules if you want. I don't know any other method.

Chew-Seong Cheong - 4 years, 8 months ago

sorry, i just saw this comment. The more divisors there are of $a_n$ and $a_0$ , the more 'manual labor' there is. G-filtered Polycules works with any $n$ . But it's real value is teaching kids (under age 15 in the United States--Junior High School) how to factor a polynomial of ANY degree while only using simple integer addition and integer multiplication. I'm currently creating 'bookend prime' polynomials of ANY degree, which is perfect for my 'tool' because primes just have the two factors. Now I can create some really cool problems. I'm working on one where a bookend prime polynomial of any degree has at least one rational factor, and where the other factor of degree $n-1$ has $n$ terms (when $x=1$ ) that sum to $1+2+...+n$ , where $n$ is the degree of the original bookend prime polynomial $bp_n(x)$ !!!

Frank Giordano - 4 years, 8 months ago

Frank Giordano
Sep 21, 2016

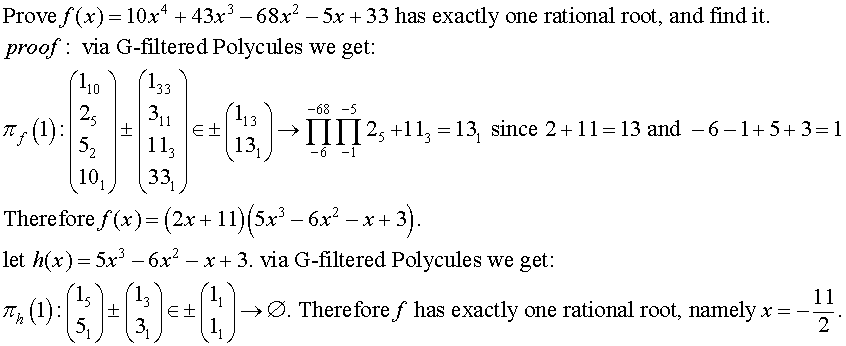They don't allow a fraction as an answer here, thus the "multiply by 100". ANSWER is -550.

this facebook video explains the Game of G-filtered Polycules for Cubics; leave a comment.

Decimal answer such as $-5.5$ is acceptable.

Chew-Seong Cheong - 4 years, 8 months ago

thanks, didn't think of that.

Frank Giordano - 4 years, 8 months ago

Sir, I don't know what this method is. Can you please suggest me some website so that I can learn about this new concept.

Tapas Mazumdar - 4 years, 8 months ago

get the latest version of "G-filtered Polycules" here: https://www.facebook.com/groups/factorthis/

Frank Giordano - 4 years, 7 months ago

Thanks a lot. I will take a look at it.

Chew-Seong Cheong - 4 years, 7 months ago

Lonely Quartic Rational Root

The answer is -550.

2 solutions

0 pending reports