Long meme Infinite sum
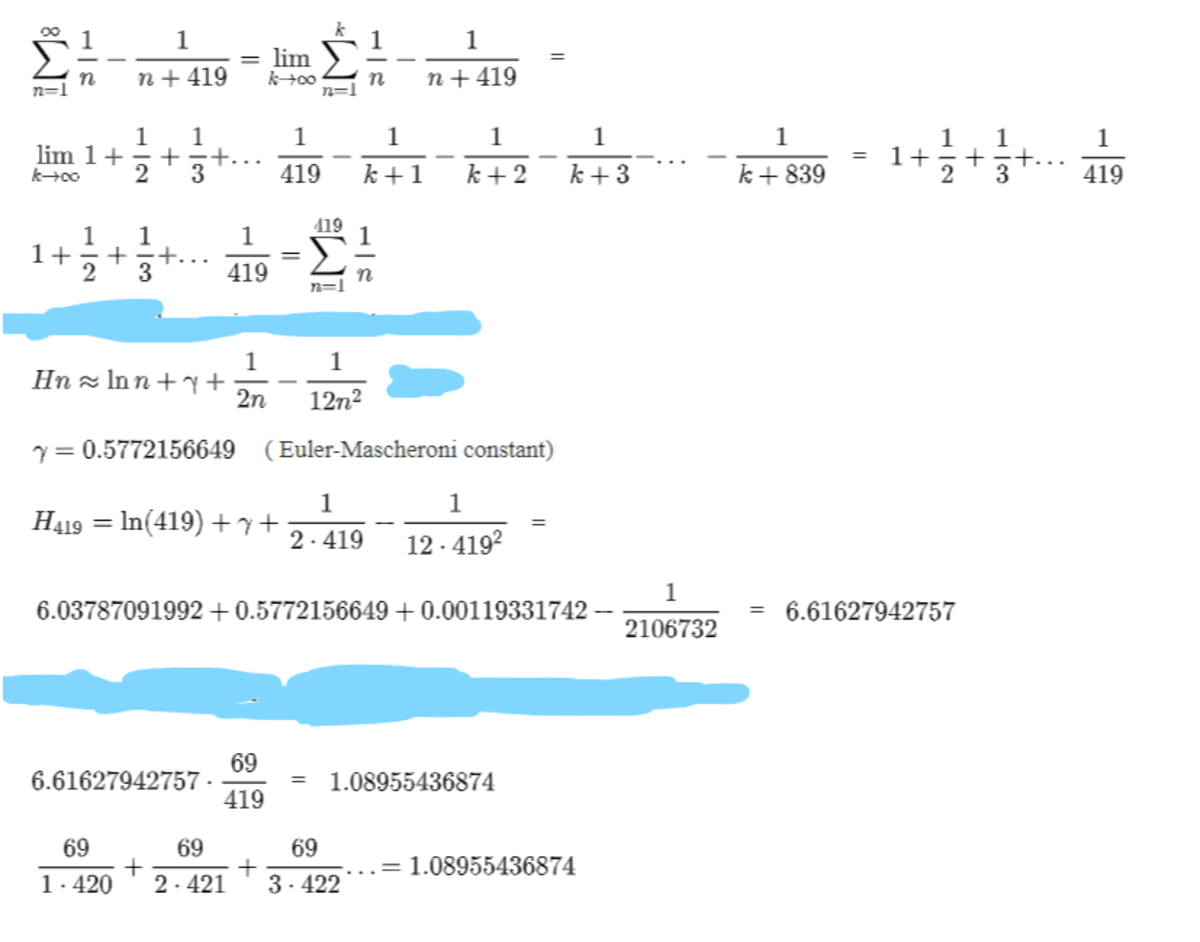
x = 1 ⋅ 4 2 0 6 9 + 2 ⋅ 4 2 1 6 9 + 3 ⋅ 4 2 2 6 9 + . . .
You can get the final answer using this site .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
x = 1 ⋅ 4 2 0 6 9 + 1 ⋅ 4 2 1 6 9 + 1 ⋅ 4 2 2 6 9 + ⋯ + n ( 4 1 9 + n ) 6 9 + ⋯ = n = 1 ∑ ∞ n ( 4 1 9 + n ) 6 9 = 4 1 9 6 9 n = 1 ∑ ∞ ( n 1 − n + 4 1 9 1 ) = 4 1 9 6 9 ( n = 1 ∑ ∞ n 1 − n = 4 2 0 ∑ ∞ n 1 ) = 4 1 9 6 9 ( 1 1 + 2 1 + 3 1 + ⋯ + 4 1 9 1 ) = 4 1 9 6 9 H ( 4 1 9 ) ≈ 4 1 9 6 9 ⋅ 6 . 6 1 6 2 7 9 4 2 8 ≈ 1 . 0 4 By partial fraction decomposition H ( n ) denotes the n th harmonic number. By Excel spreadsheet
Therefore, 1 < x < 1 . 1 .
Reference: Harmonic number
It would be better to add more info as H n ∼ γ + ln n + 2 n 1 then for n = 4 1 9 H 4 1 9 ∼ γ + ln 4 1 9 + 2 × 4 1 9 1 ∼ 6 . 6 1 6 2 7
Log in to reply
Nope, strictly everyone knows that H ∞ does not converge. The above solution purposely avoided H ∞ .