Long transmission line
Certain transmission lines can be modeled as a long 3D circuit as shown in the figure below. Here, all the the wires have equal length and electrical resistance . Determine the equivalent resistance in Ohms between the points A and B. Assume the transmission line to be infinite.
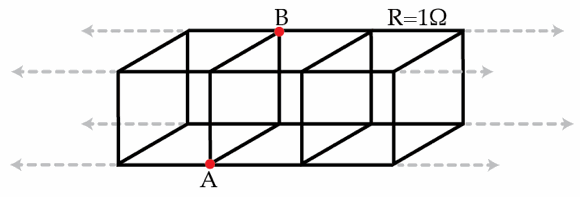
The answer is 0.577.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are four horizontal wires of infinite length. Let wires 1 and 2 be the wires that A and B are on, and wires 3 and 4 be the other two. Consider now any segment on wire 3 or 4. When we apply a potential difference between A and B , so that a current will flow from A to B , then there will be a certain current on this segment. If we now reverse the potential, the current will flow in the opposite direction. However, reversing the potential is, by symmetry of the transmission line, equivalent to reflecting the line in the plane containing wires 3 and 4. This reflection however does not alter the current in the wire segment. The only way both statements can hold (the current reverses and remains the same), is that the current in the segment is zero. Therefore, there is no current at all in wires 3 and 4. Therefore, for the purpose of this problem, we can ignore all the wire segments in wires 3 and 4.
Consider now any two points on wires 1 and 2 respectively, that are at the same horizontal location in the transmission line (like A and B ). The two short connections between these two points, going via line 3 and 4 respectively, are now each simply two wire segments in series. These two connections together are, in terms of resistance, equivalent to a single wire segment ( 2 R ∣ ∣ 2 R = R ). We can therefore make this substitution.
We now have a two-dimensional transmission line that looks like an infinite sequence of squares (in the same way that we started with an infinite sequence of cubes).
Let r be the resistance of everything to the left (or right) of the wire segment between A and B , so that we are looking for r ∣ ∣ R ∣ ∣ r . Since the line is infinite, we can freely add an extra square to the right of the segment A B . With that, we find a recursive relation for r that we can solve:
r = R + ( R ∣ ∣ r ) + R = 2 R + r + R R r ⟺ 0 = ( r + R ) ( r − 2 R ) − R r = r 2 − 2 R r − 2 R 2 ⟺ r = ( 1 ± 3 ) R ⇒ r = ( 1 + 3 ) R
The equivalent resistance between A and B is thus
r ∣ ∣ R ∣ ∣ r = ( R 1 + r 2 ) − 1 = ( 1 + 1 + 3 2 ) − 1 R = 3 R = 3 1 Ω = 0 . 5 7 7 Ω