Look at it in another way
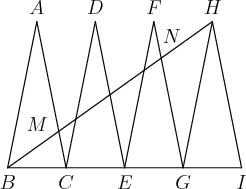 In the diagram,
△
A
B
C
,
△
C
D
E
,
△
E
F
G
and
△
H
G
I
are congruent isosceles triangles.
B
,
C
,
E
,
G
and
I
are collinear. Suppose that
A
C
and
B
H
meet at
M
and
F
G
and
B
H
meet at
N
. Given
[
H
G
N
]
=
1
0
, then the value of
[
B
M
C
]
is
n
m
for relatively prime
m
and
n
. Find
m
+
n
.
In the diagram,
△
A
B
C
,
△
C
D
E
,
△
E
F
G
and
△
H
G
I
are congruent isosceles triangles.
B
,
C
,
E
,
G
and
I
are collinear. Suppose that
A
C
and
B
H
meet at
M
and
F
G
and
B
H
meet at
N
. Given
[
H
G
N
]
=
1
0
, then the value of
[
B
M
C
]
is
n
m
for relatively prime
m
and
n
. Find
m
+
n
.
[ A B C ] denotes the area of figure A B C .
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
By the intercept theorem it's easily seen that ( B G N ) = 9 ( B C M ) and that ( B G H ) = 1 2 ( B C M ) , so that ( N G H ) = 3 ( B C M ) and eventually ( B C M ) = 1 0 / 3 . □
you can easily prove that A B C D is a parallelogram.So B C ∥ A D .repeating this for other triangles results that A , D , F , H are collinear and B I ∥ A H . So A B G H is parallelogram.taking area of △ A B C = x , area of △ B G H = 2 6 x = 3 x .So area of △ B H I = 4 x . note that A C ∥ H I ⇒ △ B M C ∼ △ B H I ⇒ ( B I B C ) 2 = [ B I H ] [ B C M ] = 1 6 1 . Now prove △ B M C ≅ △ F N H . By this we get the equation 4 x + 1 0 = x . using this we can find x and then 4 x (area of △ B M C )
First, is not hard to find out that △ B C M ≅ △ H F N . Now we set B C = b and M K = h where M K is height of △ B C M .
[ H F G ] − [ H F N ] = 1 0 ⇒ 2 b ⋅ 4 h − 2 b h = 1 0 ⇒ 4 b h − b h = 2 0 ⇒ 2 b h = 3 1 0 ⇒ n + m = 1 0 + 3 = 1 3
Construct a point J on H A with distance H F to the left of point A . Then B I H J has rotational symmetry, so △ H N G ≅ △ B M A , so [ B M A ] = 1 0 .
Note that △ B M C and △ B M A have the same height if you take M C and M A to be the respective bases. Hence, [ B M C ] [ B M A ] = M C M A .
Note that △ B M C ∼ △ H M A , so M C M A = M B M H = B M B H − 1 .
Note that △ B M C ∼ △ B H I , so B M B H = B C B I = 4 .
Therefore, [ B M C ] [ B M A ] = 4 − 1 = 3 . But we know [ B M A ] = 1 0 , so [ B M C ] 1 0 = 3 , so [ B M A ] = 1 0 / 3 , so m = 1 0 and n = 3 , so m + n = 1 3 .