Look ma, up in the sky?
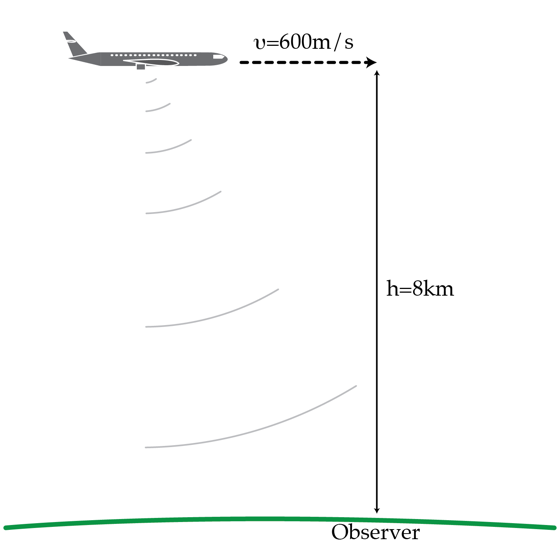
The velocity of sound in the atmosphere is c = 3 0 0 m / s . An airplane is traveling with velocity v = 6 0 0 m / s at an altitude of h = 8 k m over an observer. How far horizontally past the observer in kilometers will the plane be when the observer first hears the noise of the airplane?
The answer is 13.86.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Let the observer be at point x. Also, let the source (the plane) be originally at P at height h above the ground, moving to the right with speed v. After time t, the wave emitted from point P has traveled a distance ct (which is line Px). The source has traveled a distance vt (which is line PP'), now at P'. The line P'x from P' to the wavefront emitted when the source was at P, which is at point x makes an angle A with the path of the source, given by: sin A = ct / vt = c/v. Geometrically, there is a right triangle of legs P'x, Px; and hypotenuse PP'.
On the other hand, let x' be the point on the ground below P' (P' is at height h above the ground). Therefore the height h is the line P'x'. Visually, there would be a right triangle with legs xx' and P'x', with the hypotenuse P'x, and angle A between P'x and xx'. Therefore tan A = h/ |xx'| , where xx' is the distance horizontally past the observer in kilometers will the plane be when the observer first hears the noise of the airplane.
sin A = 300 (m/s)/600(m/s), A = 30 degrees
tan A = h / |xx'| 3^(-1/2) = 8 (km) / |xx'| |xx'| = 13.86 km
Suppose the distance to the observer plane horizontally when the sound is released is x km, then the distance sound and the observer is sqrt(x ^ +8 ^ 2). The time it takes the sound to reach the observer is the time required for plane flight runs a distance of (x + y) km. Then we obtained time t =sqrt(x ^ +8 ^ 2)/0.3=(x+y)/0.6 so we get quadratic y function that is y^2+2xy-3x^2-256=0. We get the root of y is y=2(x^2+64)^0.5-x. Use derivative y with respect to x we get minimum y is 8.3^0.5=13.856
Define plane's initial horizontal distance from the observer as a , and the distance the plane travels before the sound reaches the observer as d . The distance the sound must travel to reach the observer then is \sqrt{ a ^2 + 8^2}, so the time it takes is that divided by .3 (speed of sound converted to km/s). The distance the plane travels is that time, multiplied by .6, so the distance the plane travels is 2\sqrt{ a ^2 + 8^2}. This is the total distance the plane traveled, but some of that distance brought the plane toward the observer, so we need to subtract a from it to find the distance the plane traveled away from the observer. This gives an equation for the distance the plane gets away from the observer, so we just take the derivative and set it equal to zero, to find the minimum. From this we find that the initial distance which minimizes the final distance is \frac{8}{\sqrt{3}} and plugging that back in and rounding we find the distance traveled is 13.86.
Sorry! I don't know latex well at all, so I'm not sure why it isn't working...
Since the airplane is supersonic, we have to use the concept of the Mach angle. The velocities of the sound and of the airplane form a triangle, and so we have an angle, that we are going to call θ , such that sin θ = v c , where c is the speed of the sound that corresponds to the opposite side with respect to θ , and v is the velocity of the airplane that corresponds to the hypotenuse of this triangle. But this hypotenuse is at 9 0 ∘ with respect to the vertical line between the airplane and the observer. Therefore, we can define an angle α such that α = 9 0 ∘ − θ . But, by construction, tan α = h d , where d is the horizontal distance between the plane and the observer, and h is 8 km. Doing the math, we have
- θ = 3 0 ∘ ;
- α = 6 0 ∘ ;
- d = h tan α = 1 3 . 8 6 k m .
Here's something more about the Mach angle: Nasa Mach angle
Let t=0 correspond to the point when the airplane is directly overhead. The horizontal position of the airplane is therefore x=vt. If the airplane emits noise at some time t<0, then the noise must travel a distance of h 2 + v 2 t 2 to reach our observer on the ground. Therefore the time of arrival of the noise is
t a = t + c − 1 h 2 + v 2 t 2 .
When does the noise first arrive at the observer? This is the minimum value of t a , so we take the derivative with respect to t and solve for
t = − v c 2 v 2 − 1 h . Substituting this in for t in the arrival time gives the time of first sound,
t f i r s t = v h c 2 v 2 − 1 .
Hence the horizontal position of the airplane, x = v t f i r s t = 1 3 . 8 6 k m .
At first glance it’s a simple problem. But you're wrong, the plane’s moving faster than the speed of sound, and of course the plane will produce noisy sound every time.
I’ll define x 0 to be the horizontal distance from FlyingCow to Apip when the sound’s produced, and moo~ as the noisy sound produced.
Let’s simulate it in three case.
First, when x 0 = ∞ , very large, FlyingCow came out of howhere, and create a moo~ sound that travel directly to Apip. Unfortunately, the sound moving too slow to leap FlyingCow, and because FlyingCow also travel horizontally, x 0 decrease, next it will produce a new moo~ sound that can’t be leap by the previous sound.
When x 0 = 0, when FlyingCow is 8 K m above Apip, the sound will directly move vertically to Apip. So we can calculate time of the sound to travel,
∆ t = 3 0 0 m 8 0 0 0 m s − 1 = 3 8 0 s after the sound produce and FlyingCow will pass exactly
x = 6 0 0 m s − 1 × 3 8 0 s = 1 6 0 0 0 m = 1 6 K m .
Before we do next simulation, we need to know the shortest way of the sound to travel to Apip is a straight line from FlyingCow to Apip, so we doesn’t need a horrible curve equation.
When x 0 = 5 0 0 0 m , and 8 K m above Apip, the moo~ sound produced and at that time the sound start to travel to Apip, the distance is r = 5 0 0 0 2 + 8 0 0 0 2 ≈ 9 4 3 4 m .
∆ t = 3 0 0 9 4 3 4 = 3 1 . 4 4 6 6 7 s ,
at that time FlyingCow will travel 3 1 . 4 4 6 6 7 s . 6 0 0 m s − 1 ≈ 1 8 8 6 8 m .
So, Apip will hear this sound after it past 1 8 8 6 8 − 5 0 0 0 = 1 3 8 6 8 m .
After this case, we can imagine, the problem is like there was a race between hundres of athletes with each athlete have different time to start and different distance to finish, but in this case every athlete have same speed. So, we can predict who is the winner even the race haven't started yet.
With this, we know that there is one value of x 0 where flying cow produced the first moo~ sound that reach Apip. And of course, when moo~ sound heard by Apip, the distance of the plane will be smallest.
Next let θ be the angle between straight line from FlyingCow to Apip and horizontal line, x be the distance when moo~ sound heard by Apip.
With these assumption the sound will travel horizontally in V x = 3 0 0 cos θ and vertically in V y = 3 0 0 sin θ . Because FlyingCow’s 8 Km above Apip, so the sound must travel vertically 8000 m to reach Apip. So we got 8 0 0 0 = 3 0 0 sin θ × ∆ t
Implied, sound must be heard by Apip at ∆ t = 3 0 0 sin θ 8 0 0 0 … ( 1 )
Of course the sound must travel horizontally in this time Otherwise the sound just got stuck to the ground. So we got
x 0 = 3 0 0 cos θ . ∆ t … ( 2 )
Next we know the plane’s always traveling, so we got
x + x 0 = 6 0 0 . ∆ t
Unfortunately we have two unknown value variable x and x 0 , the main problem is where is FlyingCow’s position when Apip hear the first sound? OK, just substitute (2) to this equation, we’ll got
x + 3 0 0 cos θ × ∆ t = 6 0 0 × ∆ t
x = 6 0 0 . ∆ t − 3 0 0 cos θ × ∆ t
Substitute (1), we’ll got function of x ( θ ) ,
x ( θ ) = 1 6 0 0 0 csc θ − 8 0 0 0 cot θ
x ( θ ) function defined as the distance of FlyingCow horizontally past, when sound produced in angle θ to Apip, with domain 0 ≤ θ ≤ 9 0 . You can sketch it if you need. Or, you can use WolframAlpha, here’s the sketch . Mathematically, we can get extreme value of x where d θ d x = 0 ,
So just differentiate it we’ll got
Because d θ d csc θ = − cos θ csc 2 θ a n d d θ d ( cot θ ) = − csc 2 θ so,
d θ d x ( θ ) = − 8 0 0 0 ( − 1 + 2 cos θ ) csc 2 θ
8 0 0 0 csc 2 θ = 1 6 0 0 0 cos θ csc 2 θ , divide it with ( 1 6 0 0 0 csc 2 θ ) and we got
cos θ = 2 1 cos θ = 2 1
arccos 2 1 = 3 π
and it’s a minimum when d θ 2 d 2 x ( θ ) > 0 when θ = 3 π ,
d θ 2 d 2 x ( θ ) = 1 6 0 0 0 ( cot 2 θ csc θ − cot ( θ ) csc 2 θ + csc 3 θ )
d θ 2 d 2 x ( θ ) at θ = 6 0 has value 3 3 2 0 0 0 > 0) so, it’s proved.
So, the minimum x is x ( 3 π ) = 8 0 0 0 3 ≈ 1 3 8 5 6 m = 1 3 , 8 5 6 K m .