Looking Down Into The Earth
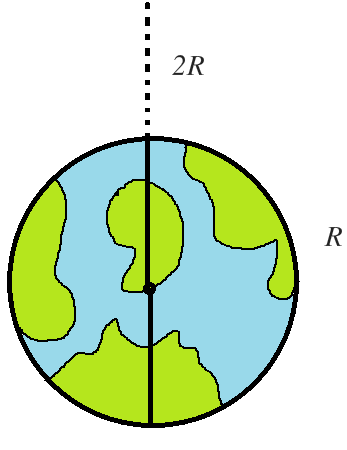
As a part of Brilliant Space Agency's New Mission, astronaut Alpha is all set to free fall under gravity, starting from rest at a point 2 R above the surface of the Earth and a tunnel has been made for him to fall through the centre and emerge out diametrically opposite from where he entered.The tunnel has been shown by the black line above.
If the time that he spends in seconds inside the earth as he falls can be represented as
α
g
R
for some real number
α
, give the value of
α
upto 3 decimal places.
Details and Assumptions
- Assume the Earth to be a perfect sphere of uniform density.
- R is the radius of the Earth and g is the acceleration due to gravity at the surface of the Earth.
- Ignore any air resistance as he enters the atmosphere.
The answer is 1.42745.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Can someone please post a solution that is much shorter and uses concept of Simple Harmonic Motion and Oscillations? Thanks.
There are two different regimes in this problem. Therefore simple harmonic motion does not apply.
Log in to reply
Thank you.
The limits of integration for calculating velocity while reaching the earth's surface is incorrect. It should be from 2R to R, and not zero. You could apply energy conservation principle rather, to calculate this velocity easily. The correct answer is π/2
Log in to reply
The limits of integration outside of the Earth are 3R down to 1R. The authors answer is correct.
I can’t type out all details as I’m short on time.
Take the center of the planet to be the origin and take the y-axis along the tunnel. We are told to assume Earth is a uniform sphere; By the famous shell theorem, the effective mass at a height y is M e f f = M ( R y ) 3 and so Newton’s law of gravity becomes m a = − ( R 2 G M m ) ( R y ) but we recognize R 2 G M as the surface gravity g , therefore we get:
a = y ¨ = d t 2 d 2 y = − R g y
This is the differential equation of simple harmonic motion with frequency R g . So the general solution is y = C 1 sin ( R g t + C 2 ) . If we then incorporate the initial conditions y ( 0 ) = R , and, y ˙ ( 0 ) = 3 − 2 g R then we get:
y = − 3 7 R sin ( R g t − arcsin ( 7 3 ) )
The answer then comes by finding the smallest t for which y = − R .
It should be noted that this simple harmonic equation for y only applies when inside the Earth. Once beyond the surface, the equation of motion changes. Nonetheless the answer is α = 2 arcsin 7 3
At height 2R above the surface, the potential energy per mass is − M G / 3 R . At the surface, the potential energy per mass is − M G / R . Because the acceleration at the surface is g = M G / R 2 , we know that the potential difference is Δ V = 3 2 g R so that the velocity at the surface is v s = 3 4 g R At distance x < R from the center, the acceleration is a = x g / R (see below), so that free fall when x<R is (a small portion of) a harmonic oscillation with angular velocity ω = g / R .
If the motion inside the earth is described by x ( t ) = A sin ω t then the velocity is given by v ( t ) = ω A cos ω t
At x = R = A sin φ we have v = v s = ω A cos φ and it follows that
tan φ = R ω / v s
so that φ = arctan ( R ω / v s ) = arctan 4 3 = arctan ( 2 1 3 )
The time spent inside the earth is from -φ/ω to φ/ω, so
Δ t = 2 φ / ω = 2 φ R / g
Since ω is in radians per second, we need to express φ in radians to find the answer in seconds. The requested answer is α = 2 arctan 2 1 3 = 1 . 4 2 7
To give an idea: suppose R = 6 . 4 ⋅ 1 0 6 m and g = 1 0 m s − 2 , then R / g = 8 0 0 s and Δ t = 1 1 4 seconds.
Here follows the derivation of the fact that the acceleration is a = x g / R , assuming uniform mass distribution. Two well-known facts are that
- inside a uniform spherical shell there is no net gravitation due to the mass of the shell
- and outside a spherical symmetric mass distribution the gravitation is just as if all mass was concentrated in the center. So when using just the mass of the earth that is closer to the earths centre than the astronaut, and do as if that's concentrated in the eaths centre, we get the right force. The mass of a sphere of radius x is M = 3 4 π x 3 ρ , and the acceleration is a = x 2 M G = 3 4 π ρ G x ; Since 3 4 π ρ G R = g we have a = x g / R .
Solutions of x ¨ = − c x are x ( t ) = e k + i ω t (i.e. iany linear combination of cos ( ω t ) and sin ( ω t ) ), where ω 2 = c .
Numerical integration used.Vacuum conditions assumed! Distance unit is meters, time using is seconds throughout this solution.
g = QuantityMagnitude [ UnitConvert [ Quantity [ 1 , Earth gravity ] , meters per seconds squared ] ] ⟹ 2 0 0 0 0 1 9 6 1 3 3
r = Round [ QuantityMagnitude [ UnitConvert [ 1 R 1 , meters ] ] ] ⟹ 6 3 7 1 0 0 9
fall = First [ y /. NDSolve [ { y ′ ′ ( t ) = − ( r y ( t ) ) 2 g , y ′ ( 0 ) = 0 , y ( 0 ) = 3 r } , y , { t , 0 , 4 5 0 0 } ] ] ;
Then, I did some manual root finding to get the fall time to the surface: 4225.223900998 seconds.
The error is fall ( 4 2 2 5 . 2 2 3 9 0 0 9 9 8 ) − r ⟹ 1 . 7 3 0 3 9 7 3 4 3 6 3 5 5 5 9 × 1 0 − 6 .
The derivative of the position, the velocity, is fall ′ ( 4 2 2 5 . 2 2 3 9 0 0 9 9 8 ) ⟹ − 9 1 2 7 . 1 2 2 3 1 1 0 8 5 2 7 .
I really hope that the astronaut does not hit the tunnel and that the aim is good enough to make it all the way through.
inside = First [ y /. NDSolve [ { y ′ ′ ( t ) = − r g y ( t ) , y ′ ( 0 ) = − 9 1 2 7 . 1 2 , y ( 0 ) = r } , y , { t , 0 , 4 8 0 0 } ] ] ;
Solve [ inside ( t ) = − r , t ] ⟹ t → 1 1 5 0 . 5 4 6 7 2 1 0 5 7 8 4 7 7 .
Check to see if we are back at the surface: r inside ( 1 1 5 0 . 5 4 6 7 2 1 0 5 7 8 4 7 7 ) ⟹ − 1 .
g r ⟹ 8 0 6 . 0 1 6 2 0 1 4 7 0 4 3 6 .
8 0 6 . 0 1 6 2 0 1 4 7 0 4 3 5 5 1 1 5 0 . 5 4 6 7 2 1 0 5 7 8 4 7 7 ⟹ 1 . 4 2 7 4 4 8 6 2 8 1 5 2 7 3 .
At the center of the Earth, the astronaut's velocity is inside ′ ( 2 1 1 5 0 . 5 5 ) ⟹ − 1 2 0 7 4 . 0 4 7 0 5 7 0 6 8 4 .
That is greater than the Earth surface escape velocity; but, of course, the astronaut has to fall out of the gravity well.
Go ahead only if you are familiar with the formulae for acceleration due to gravity at a height h and at a depth d from the surface of the earth. g h = ( 1 + ( r h ) ) 2 g ⋯ ⋯ ( 1 ) g d = g ( 1 − r d ) ⋯ ⋯ ( 2 )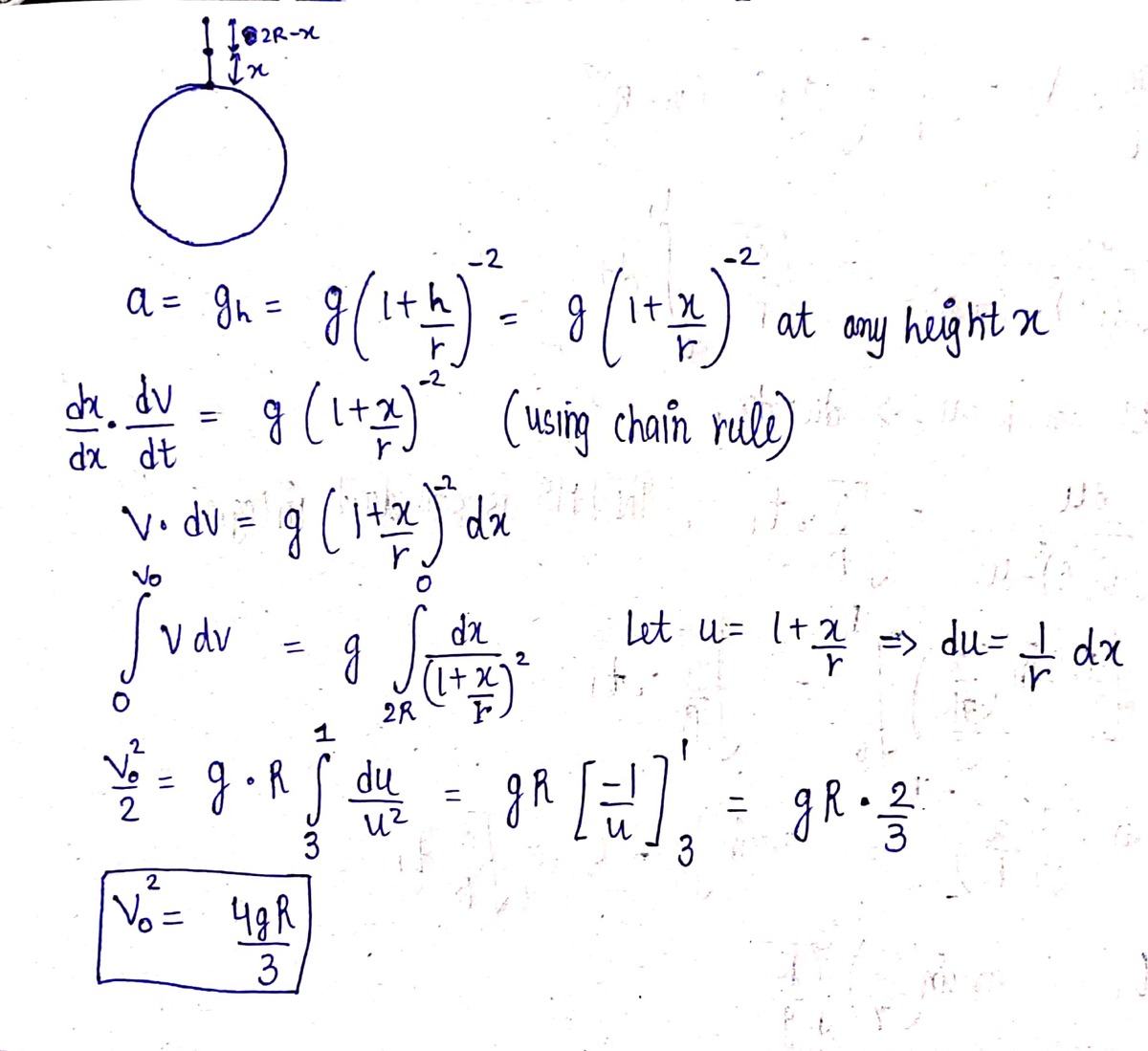 We have got the velocity with which the astronaut reaches earth.
v
0
2
=
3
4
g
R
Now we will go to the second part of the question and use
(
2
)
.
We have got the velocity with which the astronaut reaches earth.
v
0
2
=
3
4
g
R
Now we will go to the second part of the question and use
(
2
)
.
 We have obtained the velocity at any depth
x
which is
v
f
=
R
g
⋅
3
7
R
2
−
(
x
−
R
)
2
Congratulations!
If you followed till this far, you might want to complete it yourself. We will integrate this to get the time.
We have obtained the velocity at any depth
x
which is
v
f
=
R
g
⋅
3
7
R
2
−
(
x
−
R
)
2
Congratulations!
If you followed till this far, you might want to complete it yourself. We will integrate this to get the time.
 The time taken by our friend Alpha to reach the centre of the earth is
t
1
=
arcsin
(
7
3
)
⋅
g
R
Now the time taken to get from the centre to the other end is exactly the same as
t
1
, and what's more interesting is that our Alpha will exit with a velocity
v
0
. I will leave this proof to you to build your confidence that you have understood the above seemingly long steps.
The time taken by our friend Alpha to reach the centre of the earth is
t
1
=
arcsin
(
7
3
)
⋅
g
R
Now the time taken to get from the centre to the other end is exactly the same as
t
1
, and what's more interesting is that our Alpha will exit with a velocity
v
0
. I will leave this proof to you to build your confidence that you have understood the above seemingly long steps.
Now we need to find the velocity of our astronaut as he enters the earth. Till that point, the acceleration would be given by ( 1 ) .
Finally, the total time T spent inside the earth is T = 2 t 1 = 2 arcsin ( 7 3 ) ⋅ g R ≈ 1 . 4 2 7 g R
Thus α = 1 . 4 2 7