Looking for familiar limits

Calculus Level 2

If L = lim ⁡ x → 0 tan ⁡ x − sin ⁡ x x 3 L = \displaystyle \lim_{x \rightarrow 0} \dfrac{\tan x - \sin x}{x^{3}} , find 10 L 10 L .

Credit: Piskunov's Differential and Integral Calculus


The answer is 5.

View wiki
Hobart Pao by Hobart Pao , 23, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Rishabh Jain
Feb 6, 2016

U s e tan ⁡ x = sin ⁡ x cos ⁡ x and take sin x common . \small{\color{#000fff}{Use~\tan x=\dfrac{\sin x}{\cos x}\text{ and take sin x common .}}} = lim ⁡ x → 0 sin ⁡ x ( 1 − cos ⁡ x ) x 3 =\lim_{x\rightarrow0} \dfrac{\sin x(1-\cos x)}{x^3} = lim ⁡ x → 0 sin ⁡ x x × lim ⁡ x → 0 1 − cos ⁡ x x 2 =\lim_{x\rightarrow0} \dfrac{\sin x}{x}\times \lim_{x\rightarrow0} \dfrac{1-\cos x}{x^2} = 1 × 1 2 = 1 2 =\large 1\times \dfrac{1}{2}=\dfrac{1}{2} = 10 × 1 2 = 5 =\Large 10\times\dfrac{1}{2}=\boxed{\color{#302B94}{5}} lim ⁡ x → 0 sin ⁡ x x = 1 a n d lim ⁡ x → 0 1 − cos ⁡ x x 2 = 1 2 \color{#20A900}{\boxed{\color{#D61F06}{\lim_{x\rightarrow0} \dfrac{\sin x}{x}=1~and~\lim_{x\rightarrow0} \dfrac{1-\cos x}{x^2}=\dfrac{1}{2}}}}

10 Helpful 0 Interesting 0 Brilliant 0 Confused

I guess that the first numerator should be tan ⁡ ( x ) ( 1 − cos ⁡ ( x ) ) \tan(x)(1 - \cos(x)) , which will still work since

lim ⁡ x → 0 tan ⁡ ( x ) x = 1 \displaystyle\lim_{x \to 0} \dfrac{\tan(x)}{x} = 1 as well. To prove the second "red" limit for others, note that

lim ⁡ x → 0 1 − cos ⁡ ( x ) x 2 = lim ⁡ x → 0 ( 1 − cos ⁡ ( x ) x 2 ∗ 1 + cos ⁡ ( x ) 1 + cos ⁡ ( x ) ) = lim ⁡ x → 0 sin ⁡ 2 ( x ) x 2 ( 1 + cos ⁡ ( x ) ) = \displaystyle\lim_{x \to 0} \dfrac{1 - \cos(x)}{x^{2}} = \lim_{x \to 0} \left(\dfrac{1 - \cos(x)}{x^{2}} * \dfrac{1 + \cos(x)}{1 + \cos(x)}\right) = \lim_{x \to 0} \dfrac{\sin^{2}(x)}{x^{2}(1 + \cos(x))} =

( lim ⁡ x → 0 sin ⁡ ( x ) x ) 2 ∗ lim ⁡ x → 0 1 1 + cos ⁡ ( x ) = 1 2 ∗ 1 1 + 1 = 1 2 . \displaystyle\left(\lim_{x \to 0} \dfrac{\sin(x)}{x}\right)^{2} * \lim_{x \to 0} \dfrac{1}{1 + \cos(x)} = 1^{2} * \dfrac{1}{1 + 1} = \dfrac{1}{2}.

Brian Charlesworth - 5 years, 4 months ago

Log in to reply

Also like this:

lim ⁡ x → 0 1 − cos ⁡ ( x ) x 2 = lim ⁡ x → 0 4 ( 1 − cos ⁡ ( x ) ) 4 x 2 = lim ⁡ x → 0 sin ⁡ 2 ( x / 2 ) 2 × x 2 4 = 1 2 lim ⁡ x → 0 sin ⁡ ( x / 2 ) x 2 × lim ⁡ x → 0 sin ⁡ ( x / 2 ) x 2 = 1 2 × 1 × 1 = 1 2 \begin{aligned} \lim_{x\rightarrow 0} \frac{1-\cos(x)}{x^2} &= \lim_{x\rightarrow 0} \frac{4(1-\cos(x))}{4x^2} \\ &=\lim_{x\rightarrow 0} \frac{\sin^2(x/2)}{2\times \frac{x^2}{4}} \\ &=\frac{1}{2}\lim_{x\rightarrow 0} \frac{\sin(x/2)}{\frac{x}{2}} \times \lim_{x\rightarrow 0} \frac{\sin(x/2)}{\frac{x}{2}}\\ &=\frac{1}{2} \times 1 \times 1 = \boxed{\dfrac{1}{2}} \end{aligned}

PS: Trigo is cool :P

Nihar Mahajan - 5 years, 4 months ago

Log in to reply

One more method is to use Maclaurin series , i.e.,

tan ⁡ ( x ) = x + x 3 3 + O ( x 5 ) , sin ⁡ ( x ) = x − x 3 6 + O ( x 5 ) , \tan(x) = x + \dfrac{x^{3}}{3} + O(x^{5}), \sin(x) = x - \dfrac{x^{3}}{6} + O(x^{5}),

which means that tan ⁡ ( x ) − sin ⁡ ( x ) = x 3 2 + O ( x 5 ) . \tan(x) - \sin(x) = \dfrac{x^{3}}{2} + O(x^{5}).

Dividing through by x 3 x^{3} gives us lim ⁡ x → 0 ( 1 2 + O ( x 2 ) ) = 1 2 \displaystyle\lim_{x \to 0}\left(\dfrac{1}{2} + O(x^{2})\right) = \dfrac{1}{2} .

Brian Charlesworth - 5 years, 4 months ago

That is cool. I haven't seen it done that way before. :)

Brian Charlesworth - 5 years, 4 months ago

I took the LCM and placed cos0=1. = lim ⁡ x → 0 sin ⁡ x x 3 ( 1 cos ⁡ x − 1 ) = lim ⁡ x → 0 sin ⁡ x x 3 ( 1 − cos ⁡ x 1 ) . . . . . . since lim ⁡ x → 0 cos ⁡ x = 1 =\lim_{x\rightarrow0}\dfrac{\sin x}{x^3} ( \dfrac{1}{\cos x}-1)\\ =\lim_{x\rightarrow0} \dfrac{\sin x}{x^3} (\dfrac{1-\cos x}{1})......\text{since}\lim_{x\rightarrow0} \cos x=1 Anyways, nicely explained..

Rishabh Jain - 5 years, 4 months ago

Log in to reply

Ah, o.k.. That looks good, then. :)

Brian Charlesworth - 5 years, 4 months ago
Department 8
Feb 7, 2016

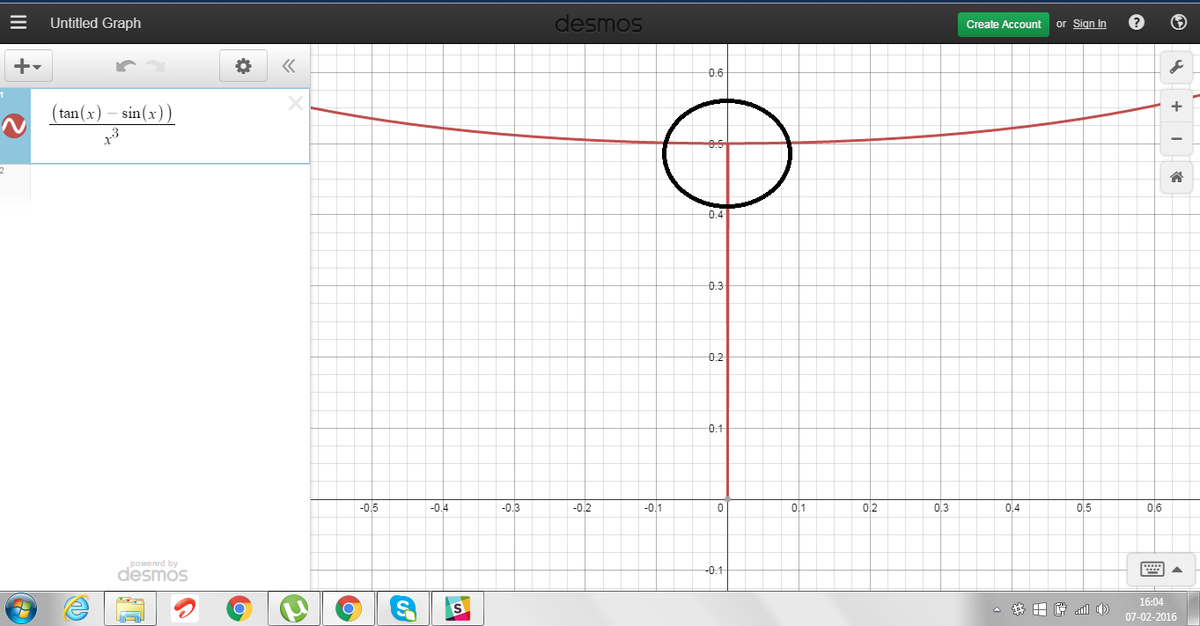
As x approaches the value pf the expression approaches 0.5

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Atul Shivam
Feb 6, 2016

Hint:- apply L'hospital rure till 0 0 \frac{0}{0} vanishes and then put limit which will gives L = 0.5 L=0.5 but we have to find 10 L 10L which is 5 \boxed{5}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

I personally found L'Hopital's for this question quite tedious...

Nihar Mahajan - 5 years, 4 months ago

Log in to reply

It's not bad when you consider that tan(0)=0 and sec(0)=1, since the only somewhat annoying derivatives that arise involve sec(x) and tan(x). With that in mind, you can ignore most of the details in calculating the third derivative of tan(x)

Tristan Goodman - 1 year, 7 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...