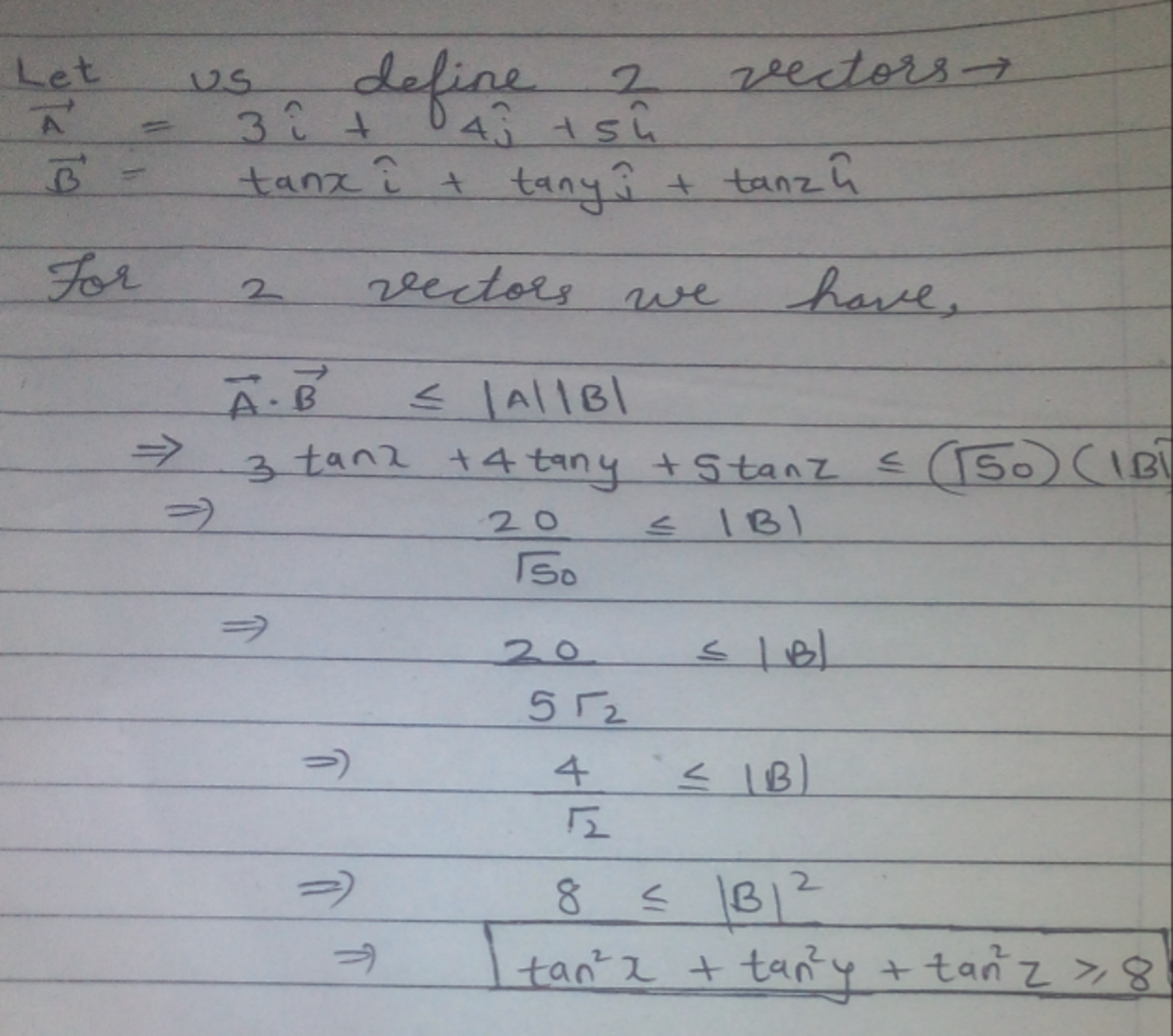Looks are deceiving.....

Geometry Level 3

Given that 3 tan ⁡ x + 4 tan ⁡ y + 5 tan ⁡ z = 20 3 \tan x + 4 \tan y + 5 \tan z = 20 . Find the minimum value of tan ⁡ 2 x + tan ⁡ 2 y + tan ⁡ 2 z \tan^2x + \tan^{2}y + \tan^{2} z .


The answer is 8.

View wiki
Dheeman Kuaner by Dheeman Kuaner , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Dheeman Kuaner
Jun 25, 2017

Was too lazy to type ....

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Its a simple application of the well known cauchy- schrawarz inequality.

Aditya Kumar - 3 years, 11 months ago
Chew-Seong Cheong
Jun 26, 2017

Relevant wiki: Cauchy-Schwarz Inequality

By Cauchy-Schwarz inequality:

( 3 tan ⁡ x + 4 tan ⁡ y + 5 tan ⁡ z ) 2 ≤ ( 3 2 + 4 2 + 5 2 ) ( tan ⁡ 2 x + tan ⁡ 2 y + tan ⁡ 2 z ) ⟹ tan ⁡ 2 x + tan ⁡ 2 y + tan ⁡ 2 z ≥ 2 0 2 9 + 16 + 25 = 8 \begin{aligned} (3\tan x +4 \tan y + 5\tan z)^2 & \le (3^2+4^2+5^2)(\tan^2 x +\tan^2 y +\tan^2 z) \\ \implies \tan^2 x +\tan^2 y +\tan^2 z & \ge \frac {20^2}{9+16+25} = \boxed{8} \end{aligned}

Equality occurs when tan ⁡ x 3 = tan ⁡ y 4 = tan ⁡ z 5 = 2 5 \dfrac {\tan x}3 = \dfrac {\tan y}4 = \dfrac {\tan z}5 = \dfrac 25 . All x x , y y , and z z exist.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...