My What A Lot Of Resistors You Have

Electricity and Magnetism Level 2

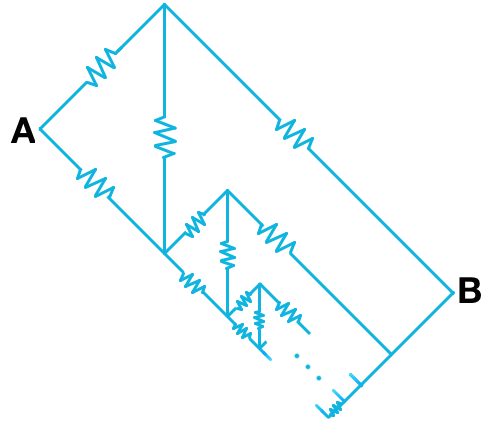
Find the equivalent resistance between points $A$ and $B$ , given that each resistance is $1 \Omega$ and the pattern continues with the same arrangement until the $176^{\text{th}}$ vertically oriented resistor, as shown in the image.

The answer is 1.

1 solution

Arjen Vreugdenhil
Jan 22, 2016

Start with the last part of the circuit: the "diamond" of four 1-ohm resistors with a fifth resistor as a bridge.

Because the circuit is symmetric, that bridging resistor is not doing anything: the points it connects have equal potentials, so that there is no current flowing through it.

That simplifies the circuit to the diamond, which is a parallel circuit of two branches of 2 ohms each.

The equivalent resistance of the last part is therefore half of 2 ohm, that is, 1 ohm.

Now this equivalent resistance is the bottom-right corner of the next part of the circuit, which once again is a diamond with a bridge. What we see is that each next part up in the circuit is identical to the previous part; every time the overall resistance is 1 ohm.

After 176 steps, we still have an equivalent resistance of $\boxed{1}$ ohm.

Challenge: What if the bottom-right resistor of the last part is not 1 ohm, but $R$ ohms?

Very good explanation, loved it.

Shubhang Mundra - 5 years, 4 months ago

Here is my answer to the challenge: If the bottom-right corner of the five-resistor diamond is $R$ , then the equivalent resistor of that diamond is $R' = \frac{5R+3}{3R+5},\ \ \ \ R'-1 = \frac{2(R-1)}{3(R-1)+8}.$ By repeating the circuit as shown in this problem, this calculation is repeated over and over. This will cause $R$ to get ever closer to 1.

Arjen Vreugdenhil - 5 years, 4 months ago

Great work , though I can verify it

Pranav Sharma - 5 years, 4 months ago

My What A Lot Of Resistors You Have

The answer is 1.

1 solution

0 pending reports