Looks like a bird...
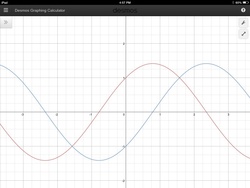 These are the graphs of
and
These are the graphs of
and
Let the area of every region enclosed by the two curves be
Find
This is part of the Sinusoidal, Cosinusoidal series
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Finding the area nearest to the origin
Finding intersection between the 2 functions
(We are only interested in the positive area)
Solving s i n ( x ) + c o s ( x ) = s i n ( x ) − c o s ( x ) gives x = 2 π There is more than 1 solution but we are only taking this solution as it is the only one useful. . . Finding the intersect between the x-axis and the two functions
We are doing so to be able to integrate with the proper limits later.
So, using some geometry, we are again able to find the intersections. s i n ( x ) + c o s ( x ) = 0 We are only interested in the smallest negative solution. s i n ( x ) + c o s ( x ) = 0 , o p p o s i t e = − a d j a c e n t This is possible when ( x = − 4 π ). . Again, using some geometry, we can solve s i n ( x ) − c o s ( x ) = 0 Here, we are only interested in the smallest positive solution. s i n ( x ) − c o s ( x ) = 0 , o p p o s i t e = a d j a c e n t This is possible when x = 4 π . . . Integrating the area
So, using the solutions above, putting in the proper limits, the area of the shaded figure above is [ ∫ − 4 π 2 π s i n ( x ) + c o s ( x ) d x ] − [ ∫ 4 π 2 π s i n ( x ) + c o s ( x ) d x ] = 2 However, this is only half of the area we want. So, A = 2 × 2 = 4 And since the question requires ( A 2 ), A 2 = 4 2 = 1 6