Looks like an spherical square in the middle

The expression derived in the sketch is for a square of one unit. The sketch is a copy of my solution for a similar problem.
So the area is $\dfrac{3-3\sqrt3+1*\pi} 3=\dfrac{a-b\sqrt c+d*\pi} e.\\$
So abcde= - 3 3 3 1 3= - 81.

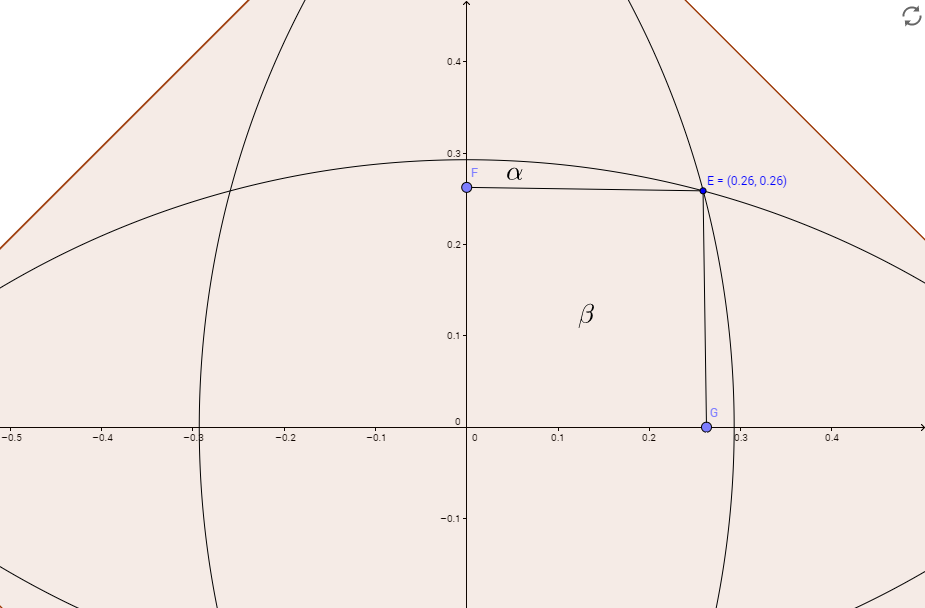
On solving eqn. no. 4 and 5 from first graph, we get point of intersection of the circles $E$ as $\left(\dfrac{\sqrt{3}-1}{2\sqrt{2}},\dfrac{\sqrt{3}-1}{2\sqrt{2}}\right)$

Required area is

$\begin{aligned} 8\alpha +4\beta&=8(\alpha+\beta)-4\beta \\&=8\int _{ 0 }^{ \frac { \sqrt { 3 } -1 }{ 2\sqrt { 2 } } }{ \sqrt { 1-{ x }^{ 2 } } -\frac { 1 }{ \sqrt { 2 } } } dx -4{ \left( \frac { \sqrt { 3 } -1 }{ 2\sqrt { 2 } } \right) }^{ 2 }\\&=8\left[ \frac { x }{ 2 } \sqrt { 1-{ x }^{ 2 } } +\frac { 1 }{ 2 } \sin ^{ -1 }{ \left( x \right) } -\frac { 1 }{ \sqrt { 2 } } x \right] \begin{matrix} \frac { \sqrt { 3 } -1 }{ 2\sqrt { 2 } } \\ \\ 0 \end{matrix}-(2-\sqrt{3})\\&\huge\color{#3D99F6}{=\boxed{\dfrac{3-3\sqrt{3}+\pi}{3}}}\end{aligned}$

What I have below is the Co-ordinate geometry approach, and hints.

Step 1: Draw 4 circles centered at (0,0) , (1,0) , (1,1) and (0,1) with their radii being 1. Also draw lines x=1 and y=1. We get that we make a figure similar to the one question describes when we look at the square formed by the co-ordinate axis and the lines x=1 and y=1.

Step 2: Find the intersection of the circles, the points which make the pints of the figure which looks circular square.

Step 3: Observe the Symmetry and divide the shape in 4 equal parts by drawing lines x=1/2 and y=1/2. And finally use integration to find the area contained between the one the four equal parts and the lines x=1/2 and y=1/2. And then multiply this value by 4.

The final answer turns out to be (pi - 3*sqrt(3) + 3)/3

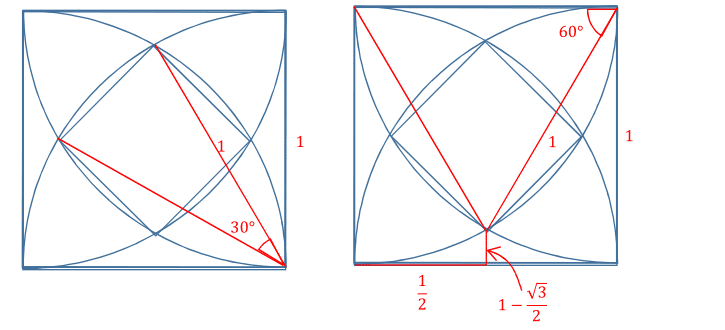The overlapping region is composed of four circular segments with central angle $30^\circ$ and radius 1 (image on the left).

Area of one of the segments is $A=\frac{R^2}{2}(\frac{\alpha\pi}{180}-sin(\alpha))=\frac{1}{2}(\frac{\pi}{6}-\frac{1}{2})=\frac{\pi-3}{12}$

Coordinates of the vertices of the square (image on the right), can be obtained as $\frac{1}{2}$ and the difference between $1$ and the height of an equilateral triangle with side $1$ , which is $1-\frac{\sqrt{3}}{2}$ .

So the points are $(\frac{1}{2}, 1-\frac{\sqrt{3}}{2})$ and $(1-\frac{\sqrt{3}}{2}, \frac{1}{2})$ and the distance between them is $s=\frac{\sqrt{3}-1}{\sqrt{2}}$ . The area of the square is then $s^2=\frac{(\sqrt{3}-1)^2}{2}$ .

Adding it all together $A=4\times\frac{\pi-3}{12}+\frac{(\sqrt{3}-1)^2}{2}=\frac{\pi}{3}-\sqrt{3}+1=\frac{3-3\sqrt{3}+\pi}{3}$