Looks like Pythagoras Theorem

For those who have 0 knowledge of number theory:

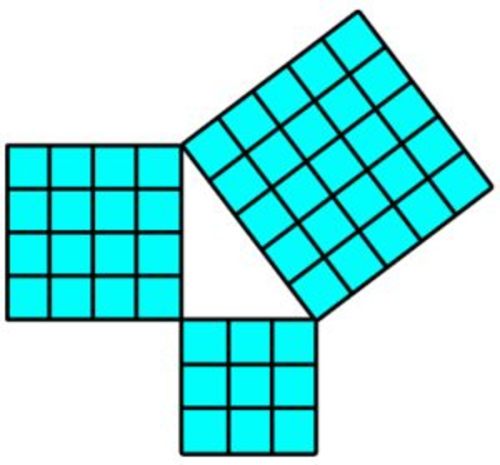15y^2 must end with 0 or 5.

15y^2 - 9 must end with 1 or 6.

7x^2 must end with 1 or 6.

x^2 must end with 3 or 8. This is not possible.

Hence, 0 solutions.

If $15x^2=7y^2+3^2$ then $7y^2+9\equiv 0$ (mod 15). Rearranging, and picking a more useful representative, $7y^2\equiv 21$ (mod 15). Then $y^2\equiv 3$ (mod 15), but 3 is not a quadratic residue of 15 (ie there is no integer whose square is equivalent to 3 mod 15). Thus there are no solutions to the given equation.

let $x=r \cos \theta$ and $y= r\sin \theta$

$\begin{aligned} 15(r \cos\theta)^2 = 7(r \sin\theta)^2 + 9\\15r^2 -15r^2 \sin^2 \theta = 7r^2 \sin^2 \theta +9 \\ 23r^2 \sin^2 \theta = 15r^2 - 9 \\ \sin^2 \theta = \frac{15}{23} - \frac{9}{23r^2} \end{aligned}$

now first of all $0 \le \sin^2 \theta \le 1$ if $\sin^2 \theta = 0$ $\begin{aligned} \implies \frac{15}{23}=\frac{9}{23r^2}\\ \implies \frac{9}{15} = r^2\\ \implies r = \sqrt {\frac{9}{15}} \end{aligned}$ since x,y are integers , so discarded,

similarly for $\sin^2 \theta = 1$ also discarded. hence number of integral solutions are $\boxed 0$