Loop #1

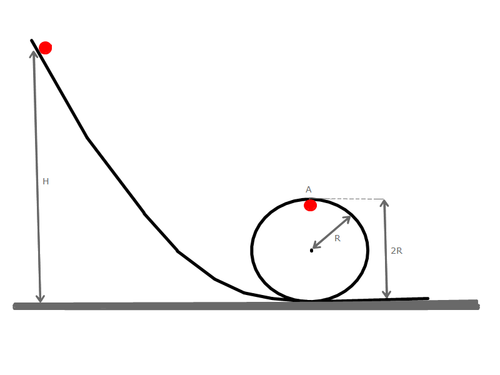Classical Mechanics Level pending

An object of mass m is droped from an height H and passes through the loop with radius R as shown in the image above. At the highest point of the loop , point A , the object exerts on the track a force with intensity equal 3 times the gravity force, 3G .

The height can be given by the following expression: H = x R

What is the value of x ?

Assume there's no friction between the track and the object.


The answer is 4.

Joel Andrade by Joel Andrade , 30, Portugal

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Joel Andrade
Jan 25, 2015

Dynamics:

At point A

− N − F g = − m a -N - Fg = -m a ,

N = 3 m g N = 3mg

a = v 2 R ) a = \frac{v^{2}}{R})

− 3 m g − m g = m v 2 R -3mg - mg = m\frac{v^{2}}{R} <=> 4 g R = v 2 4gR=v^{2}

Conservation Laws:

m g H = 1 2 m v 2 + m g h mgH=\frac{1}{2}mv^{2}+mgh <=> m g H = 1 2 m 4 g R + m g h mgH=\frac{1}{2}m4gR+mgh <=> g H = 1 2 4 g R + g 2 R gH=\frac{1}{2}4gR+g2R <=> H = 4 R H=4R

x = 4 \boxed{x=4}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...