Loop the loops - Easy

In the world of pencil puzzles, there are many puzzle types where you have to draw a loop on a lattice grid, including Country Road , Masyu , Pure Loop , Slalom , and Yajilin . In most of these puzzles (and all of the linked above), the loop visits some of the cells, passing through the cells' centers, and may not use a cell more than once (which also means no intersections, no touching itself, etc).

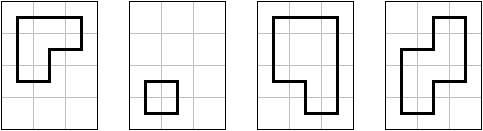
Formally, on a polyomino $P$ , a loop is a sequence of $n \ge 4$ squares $(a_1, a_2, a_3, \ldots, a_n)$ such that all squares $a_i$ are in $P$ , $a_i$ and $a_{i+1}$ share a side for all valid $i$ , $a_n$ and $a_1$ also share a side, and all squares in the loop are distinct. Loops are cyclic (it can start from any square in the loop) and don't have any orientation (reversing the loop doesn't matter), thus $(a_1, a_2, a_3, a_4), (a_2, a_3, a_4, a_1), (a_4, a_3, a_2, a_1)$ all describe the same loop.

There is $1$ loop on a $2 \times 2$ square, $3$ loops on a $2 \times 3$ rectangle, and $13$ loops on a $3 \times 3$ square. Determine the number of loops on a $3 \times 4$ rectangle.

Want a harder challenge? Try the medium difficulty .