Looped Earth
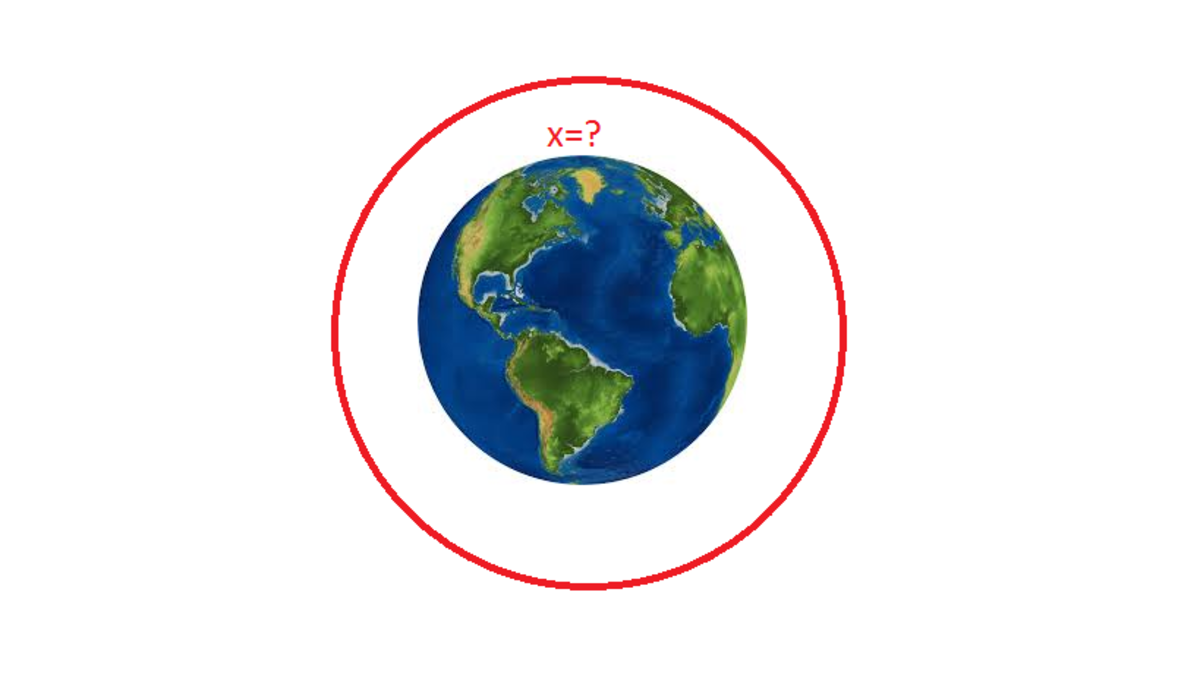Imagine the Earth as a perfect sphere. Then imagine the equator is a long belt that has been looped around the earth and fastened snugly.
If you loosened that belt by 2 meters and pulled the belt away from the surface,how much slack would there be?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
"you loosened that belt by 2 meters" meaning the circumference of belt increased of 2 meters.
The statement supposes that belt takes a new circular shape. The circumference is C=2 π *R .
We are looking for x such that newR=oldR+x gives newC=oldC+2meter.
What increasing of R (searched x) would give an increasing of C, giving 2 meter ? Developing newC(function of R) = 2 π newR = 2 π (oldR +x)
newC = 2 π oldR + 2 π x = oldC + 2 π *x.
x, increasing of R shall be such 2 π *x is the increasing of C : x= 2 π 2 m e t e r .
A calculator gives the "exact" value of x : 0,318 309 886 183 790 671 537 767 526 745 03... We have no luck π 1 is neither fractional (a/b with a and b integer) nor algebraic (solution of equation in the style 123x^57-12x^13+3=0). Man is forced to trust the machine... or to be able to calculate "by hand" series leading to the pi decimals needed...