Loops in loops
A cylindrical coil of turns, radius and length is made of a wire of resistance . We will call this coil #2. Coils #1 and #3 are identical: turns, and . We thread coil #2 through the two other coils, and bend it into a circle until the beginning and the end of the coil face each other, so that it makes a doughnut shape. The beginning and the end of the wire are connected. We arrange the three coils in a nice symmetric way as shown in the Figure.
Coil #1 is connected to a current generator that provides an alternating current of amplitude and frequency of . We measure an alternating voltage on coil #3 of the same frequency and amplitude . What is the value of in mV, rounded to the nearest integer?
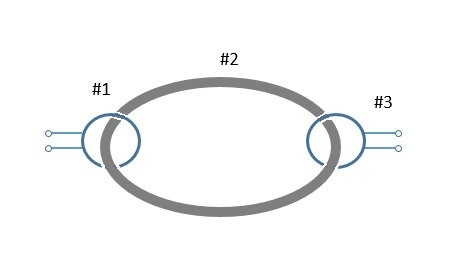
Hint: Think about the "mutual inductance" between two coils , that connects the time derivative of the current in one coil to the voltage in the other coil, . Remember, if the current and voltage terminals are interchanged the mutual inductance remains the same: .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Wil will use upper case symbols for the amplitudes and lower case symbols for the time dependent values as in i 1 = I 1 cos ω t , where ω = 2 π f is the angular frequency.
Let us first look at a more general problem, depicted on the Figure. The mutual inductance connects the emf of one coil to the derivative of the current in the other coil. For example,
u 3 = − L 2 3 d t d i 2 .
In the current situation the time derivative of the current generates a voltage u 2 in the second coil. In response to that there will be a current in the second coil, i 2 = u 2 / R . This current flows through coil #2' and its time derivative will generate a voltage U 3 in the third coil. Therefore
u 3 = d t 2 d 2 i 1 R L 1 2 L 2 3 .
Our job is to determine L 1 2 and L 2 3 . Let us start with the easy one, the interaction of coil #2 and #3 on the original Figure in the problem.
The magnetic field in a long solenoid is B = μ 0 N i / L , where μ 0 = 4 π 1 0 − 7 T / A m . The flux in that solenoid is Φ = A B = r 2 π μ 0 i N / L , where A is the cross sectional area. Therefore
u 3 = − N ′ d t d Φ = − r 2 π μ 0 L N N ′ d t d i 2 .
We can identify the mutual inductance as L 2 3 = r 2 π μ 0 L N N ′ . This is independent of the dimensions of the third coil, only the number of turns matters.
Next we need to determine L 1 2 . Let us go back to coil #3 and put the current into that coil. Can we determine the voltage in coil #2? It helps to know that there is a symmetry between interchanging the current and voltage terminals: the mutual inductance is the same, L 2 3 = L 3 2 , where L 3 2 describes how much voltage is generated in coil #2 if we drive a current into the terminals of coil #3. Note however, that coil #1 has the same properties as coil #3 and therefore L 1 2 = L 3 2 = L 2 3 . Finally we get
u 3 = − ω 2 I 1 R L 1 2 L 2 3 cos ω t = − [ I 1 ( ω r 2 π μ 0 L N N ′ ) 2 / R ] cos ω t .
With u 3 = U 3 cos ( ω t − 1 8 0 ∘ ) we get the amplitude U 3 = I 1 ( ω r 2 π μ 0 L N N ′ ) 2 / R = 9 . 9 5 m V ≈ 1 0 m V .