Before Going Forward, You'll Need To Go Back
If x is a positive real number satisfying x 2 + x 2 1 = 1 4 , find x 3 + x 3 1 .
The answer is 52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Why did you use ( x + x 1 ) 2 ?
Log in to reply
He's using the fact that the given expression x 2 + x 2 1 is equivalent to ( x + x 1 ) 2 − 2 . This allows him to calculate that x + x 1 = 1 4 + 2 = 4 from the given information, and then substitute this into his first equation (which consists of multiplying x + x 1 by x 2 + x 2 1 − 1 , giving the answer as 4 × ( 1 4 − 1 ) = 5 2 and hence solving the question).
Da condição ( x 2 + x 2 1 ) = 1 4 , tiramos que:
( x 2 + x 2 1 ) = 1 4 ( x + x 1 ) 2 − 2 = 1 4 ( x + x 1 ) 2 = 1 6 ( x + x 1 ) = 4
Com efeito,
( x 2 + x 2 1 ) ⋅ ( x + x 1 ) = x 3 + x x 2 + x 2 x + x 3 1 1 4 ⋅ 4 = x 3 + x + x 1 + x 3 1 5 6 = ( x 3 + x 3 1 ) + ( x + x 1 ) 5 6 = ( x 3 + x 3 1 ) + 4 ( x 3 + x 3 1 ) = 5 2
( x 3 + x 3 1 ) = x 2 + x 2 1 + 2 ⋅ ( x 2 + x 2 1 − 1 ) = 1 4 + 2 ⋅ ( 1 4 − 1 ) = 1 6 ⋅ 1 3 = 4 ⋅ 1 3 = 5 2
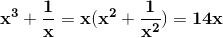
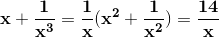
Adding the equations together we get:
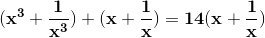
Notice that:
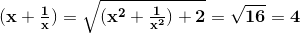
From here we get:
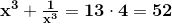
[ x 3 + ( x 1 ) 3 ] = ( x + x 1 ) ( x 2 − 1 + ( x 1 ) 2 ) . . . . . . . . . ( 1 )
( x + x 1 ) 2 = x 2 + ( x 1 ) 2 + 2
( x + x 1 ) 2 = 1 6 , Now ( x + x 1 ) = 4
Hence put it in equation to get [ x 3 + ( x 1 ) 3 ] = 5 2