Lost in the circle
O is the center of the circle to the right.
Find, in degrees, ∠ Q P R + ∠ O R Q .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
23 solutions
why does angle QOR = 2 * angle QPR???????
Log in to reply
Because in a circle, angle subtended by an arc at the centre is twice the angle at any other point on the circle. It is a theorem..!
Log in to reply
I have forgotten that theorem :D It's so long but, thanks God, I can prove that. :)
you missed something... if the angle is acute then it will be half of angle made at center and if the angle is obtuse then it will be 2ice as the angle at center. :) Thank you.
Inscribed angle theorem
We can also construct an angle QXR, X is a point on the circle, such that seg XR is diameter which will make triangle RQX a right angled triangle angle Q=90°. So angle X+angle R=90° ie x°+y°=90°
OQ=OR so angle ORG = angle OQR ,, i.e both are "x",.......
Angle QOR+ Angle OQR+ Angle ORQ=180
Angle QOR+ x+x=180
Angle QOR = 180- 2x.......................equ 1
but angle QOR=2 times Angle QPR so Angle QOR= 2 y 180-2x=2y x+y=90
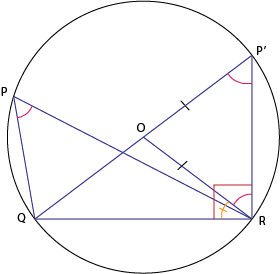 ∠QPR = ∠QP'R = ∠ORP'
∠ORQ + ∠ORP' = 90°
Hence ∠ORQ + ∠QPR = 90°
∠QPR = ∠QP'R = ∠ORP'
∠ORQ + ∠ORP' = 90°
Hence ∠ORQ + ∠QPR = 90°
Looks very elegant! :)
The angle subtended by an arc at the centre is twice the angle subtended by it anywhere else in the circle.
Thus, ∠QOR = 2∠QPR. As ∠QPR= x, therefore ∠QOR= 2x.
Now consider ∆QOR.
OR and OQ are both radii of the circle. Thus, ∆QOR is an isosceles triangle. Angles opposite to equal sides of a triangle are always equal.
Thus ∠ORQ = ∠RQO
But as ∠ORQ= y,
∠RQO = ∠ORQ = y.
Now, using the Angle Sum property of a triangle,
∠QOR + ∠ORQ + ∠RQO = 180 degrees
Substituting in ∠QOR=2x, ∠RQO = y, ∠ORQ = y, we get
2x + y + y = 180°
2x + 2y = 180°
x + y = 90°
Quad Erat Demonstratum.
thnks ishan mishra u remind me my school life
Log in to reply
Should read Quod erat demonstrandum. Not Quad.
Without loss of generality, slide P clockwise around the circle, until PR overlaps with OR. Now △ PQR is a right triangle, with ∠ PQR = 90 ∘ . Hence ∠ QPR + ∠ ORQ = ∠ QPR + ∠ PRQ = 90 ∘
if QOR = X then QPR = 1/2 X, and ORQ = (180 - X)/2 = 90 - (1/2)X Adding gives us:
1/2 X + 90 - 1/2 X = 90
90.(angle ORQ = y & QPR = x therefore angle QOR= 2x because angle subtended by a chord at the center is double the angle subtended by it at any other point on the circle. Now in triangle OQR, angle ORQ =angle OQR = y because OQ and OR are the radius. so 2x +2y = 180. so x + y = 90. and angle ORQ + angle QPR = x + y =90 degree.!!
2(ORQ)+(QOR)=180 (QOR)=180-2(ORQ) * (QPR)=0.5(QOR) (QOR)=2(QPR) * 180-2(ORQ)=2(QPR) (QPR) +(ORQ)= 180\2=90
angle QPR=x angle QOR=2x(central angle) angle OQR=angle ORQ=y thus 2x+2y=180 therefore x+y=90(dividing by 2)
Using radius of circle, triangles OPQ, OQR and OPR are isosceles. Hence, ∠ORP =∠OPR (Let it = A). so, ∠ROP = 180 - 2A (=∠QOP + ∠ROQ).
In triangle OPQ, ∠QOP = 180 - 2(x + A).
In triangle OQR, ∠ROQ = 180 - 2(y)
We said ∠ROP =(∠QOP + ∠ROQ)= 180 - 2A, so......substitute equations for angles
(180 - 2(x+A)) + (180 - 2(y)) = 180 - 2A
Rearranging gives x+y = 90. How I worked it out :p (I'm sure there's an easier way)
Incomplete set of given data. Without constraints, points P, Q, and R can be placed anywhere on the circle, thus, varying the proportions and values of the angles.
While you are correct in saying the exact value of each angle may differ from case to case, the sum of x and y will always be the same. This is due to the properties of the circle we're applying.
∠ O Q R = ∠ O R Q = y ⟹ ∠ Q O R = 1 8 0 − 2 y = 2 x ⟹ x = 2 1 8 0 − 2 y = 9 0 − y
⟹ x + y = 9 0 − y + y = 9 0 ∘
Atention! They've marked in pink something wrong (PRQ instead ORQ). That can trick you...
Since we have choices, angle Q is greater than 90 degrees and a triangle is equal to 180 degrees, so it must be the sum of the 2 other angles is less than or equal to 90 degrees..
Since both triangles QRP and QRO have the same base, the angle subtended by an arc in the centre is twice the angle subtended by this arc anywhere on the circumference. Hence, ∠ R O Q = 2 × ∠ R P Q . Since R O = Q O , ∠ Q R O can be written as 2 1 8 0 − 2 × ∠ R P Q If we then add ∠ R P Q to the result: 9 0 − ∠ R P Q + ∠ R P Q = 9 0
As point Q is moved towards R angle ORQ approaches a 90 degree angle and RPQ approaches 0 and as point Q moves towards point P the opposite happens. Given the angle choices 90 was the obvious solution.
Angle OQR=Angle ORQ[ OQ=OR, radii of same circle ] But angleORQ=y, so angle OQR=y. Now angle QOR=180-2y and angleQPR=1/2QOR. So we get 180-2y/2=x. On solving this equation, we get 90-y=x. So, x+y=90
Angle ROQ=2x y=180-2x/2 x+y=x+180-2x/2=2x+180-2x/2 =180/2=90
QOR=2QPR & OQR=ORQ, from triangle, QOR, QOR+OQR+ORQ=180, OR, 2QPR+ORQ+ORQ=180, OR,2QPR+2ORQ=180, OR,x+y=90
The angle at the center that is subtended by an arc is twice any angle subtended by the same arc anywhere else in the circle. Since ∠ Q O R is subtended by Q R , and is at the center of the circle, that means that ∠ Q O R = 2 ∠ Q P R since ∠ Q P R is also subtended by Q R . Since O Q and O R are both radii of the same circle, they are congruent. Because of this, the triangle that they create with Q R is an isosceles triangle. Since the base angles of an isosceles triangle are always equal, ∠ O Q R = ∠ O R Q . We now have the 3 angles in Isosceles triangle Q O R : ∠ O Q R , ∠ O R Q , and ∠ Q O R .
Finding x: We can use the substitution property to replace ∠ Q P R with x , so we now get the statement ∠ Q O R = 2 x .
So now we have isosceles triangle Q O R . If we were to add the three angles in it, we'd get 2 x (from the vertex angle, ∠ Q O R ) + y + y (Because there are two base angles, which both equal y since they are equal). Because the sums of the interior angles of a triangle is always 1 8 0 ∘ , we can create the simplified equation 2 x + 2 y + 1 8 0 . All we have to do now is divide both sides by 2 to get the equation x + y = 9 0 . So now it is clear to see that 90 is the answer!
Since we know the angles opposite to the equal sides of a triangle are equal so, angORQ=angOQR. Again angQOR=2angQPR. Now, Q+O+R=180. or, 2y+2x=180 Therefore, x+y=90 degrees.
QPR=x OQR=2x ORQ=(180-2x)/2=90-x=y
x+y=x+(90-x)=90
x=1/2 O (because any angle suspended by an arc on any point of circle is half to that of angle suspended by that arc in the centre ). Q=R now, O+Q+R=180 therefore, y= 180-O/2
therefore, x+y= 90-(O/2)+(O/2) thus, x+y= 90
2x + 2 y = 180 so.... x + y = 90
The angle ∠ R Q O = ∠ O R Q , and ∠ Q O R = 2 ∠ Q P R . Thus 2 ∠ O R Q + 2 ∠ Q P R = 1 8 0 ∘ , hence ∠ Q P R + ∠ O R Q = 9 0 ∘ .