Lost in the Woods
You’re lost in the woods, and your only hope of reaching civilization is to find your way back to the only road.
- You know you are exactly 1000 meters from the infinitely long, straight road.
- You have perfect relative bearings, are able to track your position perfectly, and can travel along any line or curve.
- You don't know the direction of the road and cannot see it until you are upon it.
What is the shortest possible walking distance , to the nearest meter, that will ensure you reach the road?
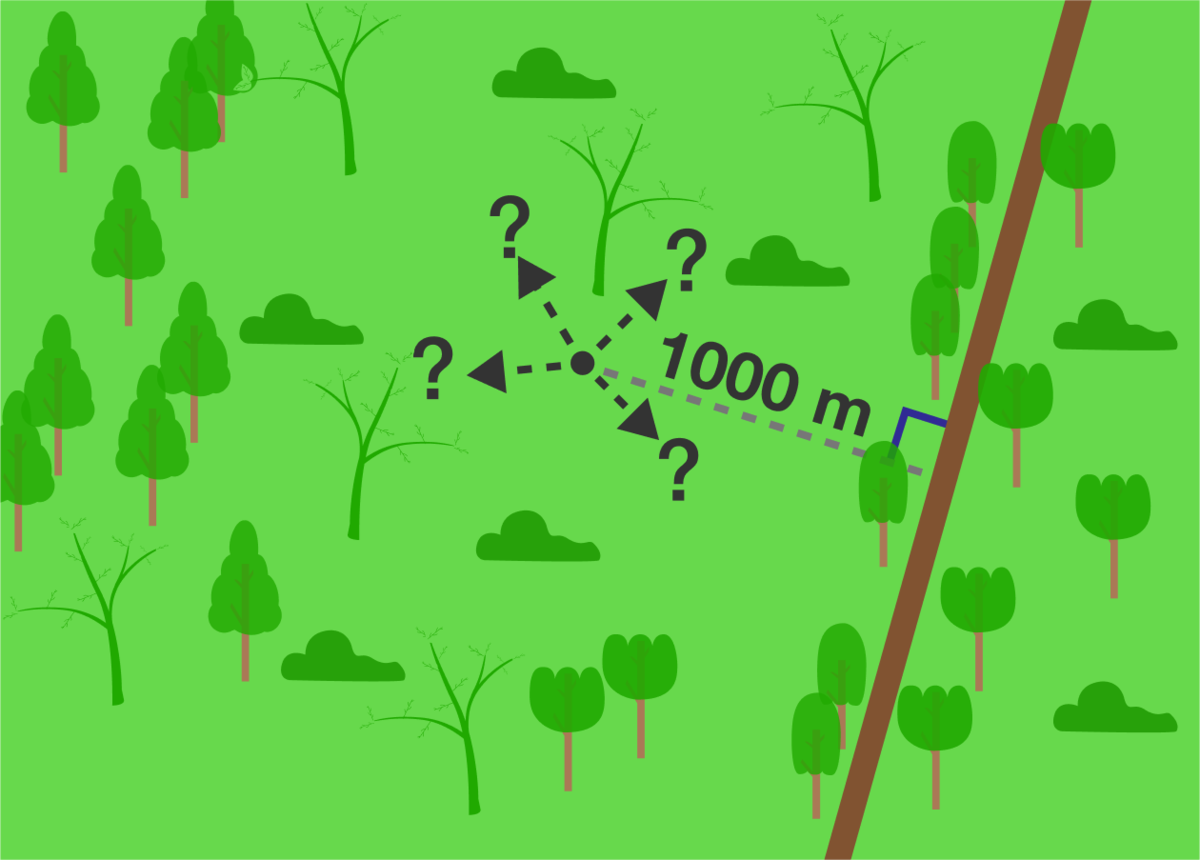
Be warned , your initial thoughts may need to be refined to truly minimize the length of your path.
The answer is 6397.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
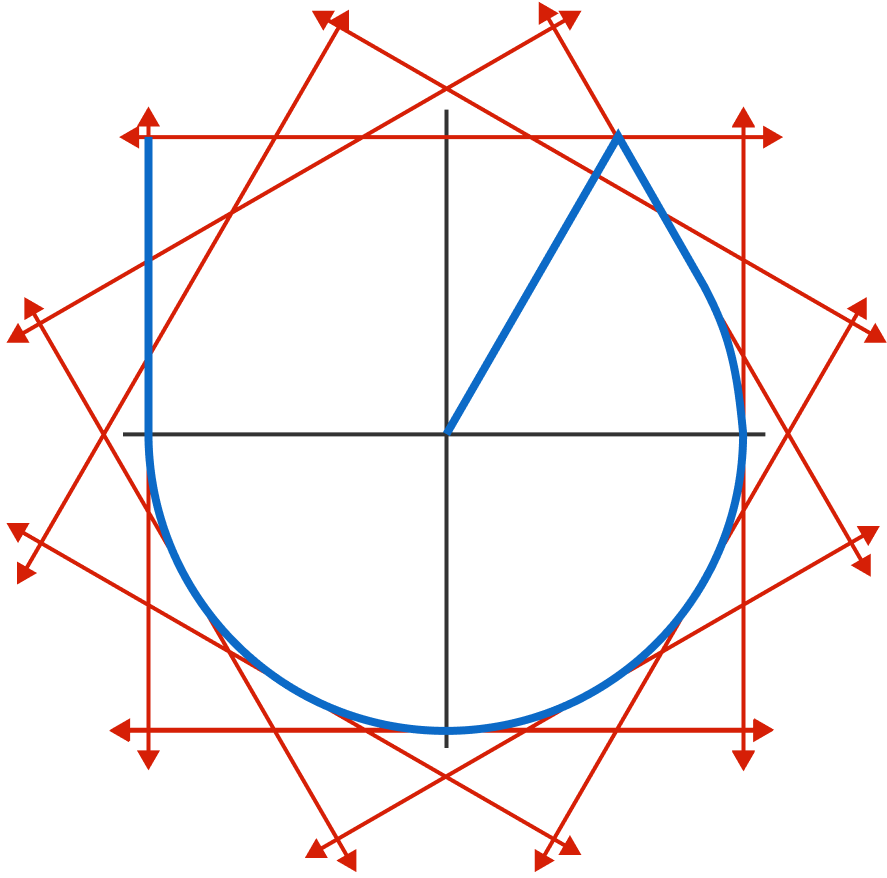
As you can see, the path given in the solution intersects with every possible road 1000 m away from the starting location:
Good problem in essence, although quite confusing in the problem description. I think it should be added that you can't see the road until you are on it, as this could cause a change in a deliberate direction, which would alter the length depending on the positioning of the road
Log in to reply
Good point, I added a clause about not being able to see the road. Is there anything else confusing? You've seen the solution so you know what it's getting at. It the picture misleading because there is really only one road?
Log in to reply
The solution is very good to clear things up as I wasn't sure so clicked Discuss Solutions. It could maybe be confirmed that the 1000m in the question is the shortest(/perpendicular to be blatantly obvious but shortest will imply this) distance to the road.
How can you show that this solution is the shortest distance required?
Log in to reply
Not exactly but I've spent a lot of time on this problem. How about this:
Would you agree if you could start anywhere you could make the right look like the left and this would be optimal? OAB is what you have to do to start from the center which you can prove with a bit of calculus.
Log in to reply
Could you tell me how you aproached that in detail? Even after this explanation I have no idea how you even approached this problem.
This solution needs pictures
So you showed that 6397 is achievable. But there is zero proof that this number is indeed the shortest path. I do not understand why should it be accepted as a formal solution to a mathematical problem.
Log in to reply
There is. See @Mark Hennings 's answer.
Log in to reply
External link to non publicly available article is also hard to consider a normal mathematical solution on the educational site. Also it is a separate answer upvoted way less then this one with zero proof of anything at all..
oh i got 6700 just the angle problem i used 45 degrees
it wont work, lets say worst case is you walk 180 deg from road, you need to choose direction and walk circular path, but lets go back, worst case cant be 180 deg from the road, lets say you walk towards the road slightly off the direct bearing, and you are almost upon it without knowing, and again you choose your circular path, if you choose right, you are there in a few meters, but if you are wrong, you basically walk all the way around a whole circumference of the circle, thus giving worst case 1000m plus circle circumference of 2000x3.14
Log in to reply
Not sure why you don't agree that 6397 is the solution. It's less than 7283m which you are proposing. Let's just take your proposal and consider the worst case - that you are 0.1° out.
After navigating 3/4 of the circle, you'll find that road sooner by walking directly "north" (or whichever direction you first walked) than by completing the 1/4 of the circle.
The same goes for the first stage of the journey. By walking a little beyond the 1000m point then plotting a tangential route back to the circle, you save on shoe leather.
Elegant. But how did you derive this?
Walk 1000 m in any direction and then walk a circle with center at the initial tracking position. This add exactly 3141 m, totaling 4141 m max until finding the road. I assume that since you can track your position is because you have a GPS and so walking a circle path with center at the original position is not difficult.
Log in to reply
The circumference of the circle is 2 0 0 0 π
Dear moderator, I can see that the solution described works; however, I see no proof that it is the shortest solution. J.R. Isbell has published a proof, but I am unable to read it because I don’t have the necessary subscription. I really would like to see a real solution to this problem. So far all of the solutions are only guesses since none of them prove that the path described is indeed the shortest.
Log in to reply
Would you agree that, if you start on the "circle", the shortest route is to track 3/4 of the circle then follow the tangential path to cover all possible roads in the final quadrant?
After that, the final part is a relatively simple calculus problem.
Dear Humphreys, My calculus teacher onced gave us Isbell's work for further reading. I can share it to you if you still need it.
This result was initially proved by J.R.Isbell here in 1957.
Your link doesn’t display anything. Is there something wrong with my browser?
Log in to reply
The link works for me. If you want to read the whole paper it will set you back $35..
Log in to reply
Is it not possible for anyone to see the solution and tell us?
Thank you, but without a subscription you can only see the first page of his paper and the proof is not on that page.
Log in to reply
True, but that paper is not available elsewhere. Take it up with Wiley Online if you want.
Just to add to the solutions provided, the first step in the chosen route identifies an angle, x and traces a route similar to the ones shown of 1/cos (x) away from the starting location then sin (x)/cos (x) back to the circle.
The distance saved traversing the circle is 2x which leaves a simple case of minimising the route which we do by differentiating the equation:
(1+sin(x))/cos(x) -2x
Working through the maths this gives 1 + sin x = 2 cos(x)^2,
=> x=30°
Using Jeremy's figure, let's say you go in some direction until you think you've gone far enough, and then turn back, thus possibly just missing a road, which is DA. Then if you travel on a circle of radius 1000 meters, you will touch all the places where the road can be until you are at C and headed back in the direction of road DA. CD is the shortest path to that road. So, the problem remains to be solved is the shortest distance from O to A to B to any point on the circle of radius 1000 meters. For shortest path, the angle OA mades with line DA is the same with the angle BA makes with line DA, and line AB should be tangent to the circle of radius 1000.
Given any line DA tangent to the circle, if one goes from O to any point on line DA, thence around the circle, and then back any point on line DA, this is the shortest posssible path.
1st you need to walk in a direction 1000m, then turn 90degrees in a direction left or right to start walking on the edge of a hypothetical circle, thus the distance traveld to ensure u reach the road is antything between 1000 and 1000 plus 2000 x 3.14, as for calculating a deffinate shortest distance, this problem is flaud
You want to ensure you reach the road, so by your method only walking 1000 plus 2000 x 3.14 would guarantee hitting the road.
Log in to reply
Yes my method guarantees hitting the road, but there is no way of finding the right bearing to walk the shortest distance, therefore the distance walked can only be variable as u can walk 2500 or 5000, but it will be in anything between the numbers i gave, as u can either walk straight to the road if you lucky, ans it can take you almost full circle to reach
In this picture 10 units = 1 0 0 0 meters.
Basically, you need to ensure you hit every tangent to an imaginary circle. You begin at the center, O, and this circle has radius 1 0 0 0 m .
Pick a reference direction and call it "north". Turn 30 degrees to the east of north and walk 3 2 0 0 0 ≈ 1 1 5 4 . 7 0 m to point A.
Next turn 120 degrees to the right and walk 3 1 0 0 0 ≈ 5 7 7 . 3 5 m to point B. You are now 1000m from the start but at an angle 60 degrees east of north.
Next walk 1 2 7 of the way around this imaginary circle of radius 1 0 0 0 m to point C.
Finally, walk 1 0 0 0 m due north to point D.
Total distance is 1 0 0 0 3 + 6 7 0 0 0 π + 1 0 0 0 ≈ 6 3 9 7 m
There seems to be a lot of interest in proving this is the optimal solution. I'm not sure I could prove it. J. R. Isbell did find and prove this path is optimal in 1957. The best I can do is feel proud that I was able to find it independently.
I can share my thought process (as I recall it from a couple of years ago)
Clearly, one way to guarantee to find the road is to go 1000 meters in some direction (it may as well be called north) and then walk a full circle.
Ok, can I do better? Think about the road as possible tangents. Well, at the end of the route instead of the last quarter circle you could go due north. This saves you some walking as π / 2 < 1 . This is segment CD.
But we can't do that at the start. Well, we sort of can if we go exactly North-East for 1 0 0 0 2 . Then due south for 1000 to hit the circle. This saves a bit because 2 < π / 2 . These portions were then refined.
What if we went up at some other angle, maybe more North than East as sort of a balance between the two other ideas. Pick a point A somewhere at the y=1000 line, walk to A and then back to the circle at B. I'm pretty sure I used calculus to minimize the two segments and the small bit of arc.
That brought me to the solution I found. I tried also making the curved path to C shorter or longer. I also tried making D higher or lower in hopes of adjusting A, but this didn't help either. When I reported my findings to the person who showed the problem to me, they indicated it was the solution.