Lost inside a convex hull!
An ant is trapped inside a convex hull shape with vertices and an area of 1.
The ant wants to walk out of this shape by following a predetermined path, which guarantees that the ant will be able to eventually escape. What is the minimum length of such a path?
Give your answer to 3 decimal places.
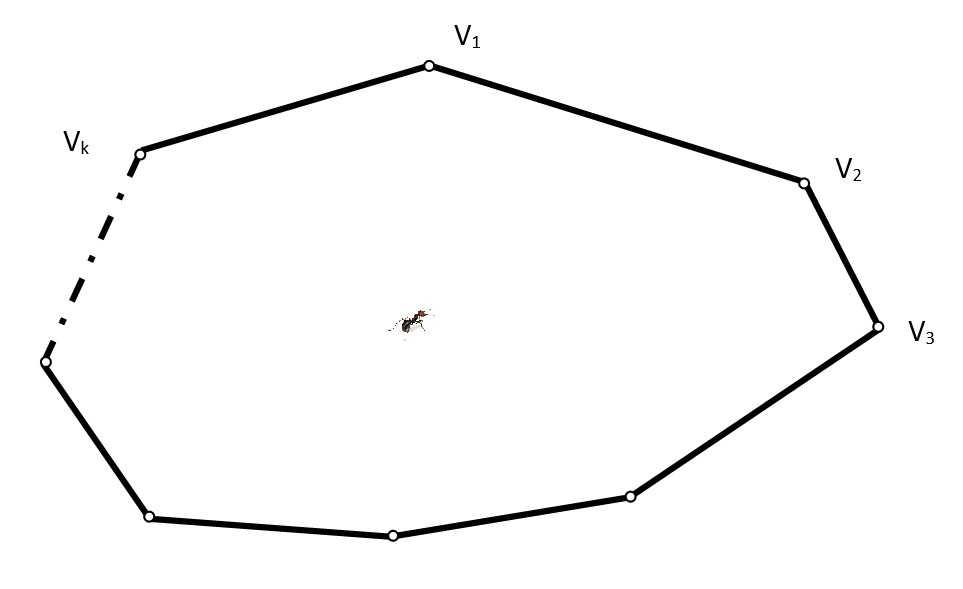
Note: If the path was along a straight line, then there is no minimum length that would guarantee the ant will be able to eventually escape.
The answer is 2.506.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!