Lots of geometrical coincidences

Let $\angle ABC=\theta$ . We add a point $F$ such that $AC$ is parallel to $BF$ and $AB=BF$ . Considering that $AB=BD$ , it follows that $\angle BAD=\angle BDA=\frac{\pi-\angle ABD}{2}$ . Moreover, $AC$ being parallel to $BF$ tells us that $\angle BAD+\angle ABF=\pi$ or $\angle BAD+\angle ABD+\angle DBF=\pi$ . Therefore $\angle DBF=\pi-\angle ABD-\angle BAD=\pi-\angle ABD-\frac{\pi-\angle ABD}{2}=\frac{\pi-\angle ABD}{2}=\angle BAD$ .

As given in the question, $AD=BE$ and we stipulate that $AB=BF$ . Considering that $\angle BAD=\angle FBE$ , we conclude that $\triangle BAD$ is congruent to $\triangle FBE$ employing $SAS$ congruence. This tells us that $\angle ABD=\angle BFE=\angle BFC-\angle CFE=\angle BAD-\angle CFE$ . Note that $\angle BFC=\angle BAD$ being opposite angles in rhombus $ABFC$ .

Considering also that $\angle BAD=\frac{\pi-\angle ABD}{2}$ :

$\angle BAD=\frac{\pi-(\angle BAD-\angle CFE)}{2}$

$2\angle BAD=\pi-(\angle BAD-\angle CFE)$

$2\angle BAD+\angle BAD-\angle CFE=\pi$

$(2+1)\angle BAD=\pi+\angle CFE$

$3\angle BAD=\pi+\angle CFE$

Considering that $AB=AC$ and hence $\angle ACB=\angle ABC$ in $\triangle ABC$ , $\angle BAD=\angle BAC=\pi-\angle ABC-\angle ACB=\pi-2\angle ABC=\pi-2\theta$ . Then:

$3(\pi-2\theta)=\pi+\angle CFE$

$3\pi-6\theta=\pi+\angle CFE$

$6\theta+\angle CFE=2\pi$

A final observation to make is this:

• Considering that $AB=BD$ , $AB=AC$ and that $AC=CE$ as given in the question, it then follows that $BD=CE$ and $CE=EF$ .
• Considering that $AB=AC=BF$ and that $AC$ is parallel to $BF$ , we see that $ABFC$ is a rhombus so that $CF=AB=AC=BF$ . Then considering that $AC=CE$ , $CF=AC$ means that $CE=CF$ .

Combining $CE=CF$ and $CE=EF$ , $\triangle CEF$ is equilateral with $CE=CF=EF$ . This means $\angle CEF=\angle ECF=\angle CFE=\frac{\pi}{3}$ . Therefore:

$6\theta+\frac{\pi}{3}=2\pi$

$6\theta=\frac{(6-1)\pi}{3}$

$6\theta=\frac{5\pi}{3}$

$\theta=\frac{5\pi}{6\times 3}$

$\theta=\frac{5\pi}{18}$

So $p+q=5+18=\boxed{23}$

.

For simplicity, take $AB = 1$ . Also, let $∠DCE = θ$ . Since $BD = AB = AC$ and $AD = BE$ , $ED = BD - BE = AC - AD = CD$ , meaning that $△CDE$ is isosceles. Then, $∠DEC = θ$ as well, and by the External Angle Theorem, $∠BDA = 2θ$ .

We use the fact that $AD + DC = AC = 1$ and write $AD$ and $DC$ in terms of $θ$ to obtain an equation in $θ$ .

Because $△BAD$ is isosceles, the perpendicular from $B$ bisects $AD$ , so $AD = 2 BD \cos{2θ} = 2 \cos{2θ}$ . Likewise, since $△DCE$ is isosceles, the perpendicular from $D$ bisects $CE$ , so $DC = \frac{\frac{CE}{2}}{\cos{θ}} = \frac{1}{2 \cos{θ}}$ .

Then, we have that $\frac{1}{2 \cos{θ}} + 2 \cos{2θ} = 1$ .

Using the identity $\cos{2θ} = 2 \cos^2{θ} - 1$ , multiplying both sides by $2 \cos{θ}$ , simplifying, this becomes $8 \cos^3{θ} - 6 \cos{θ} + 1 = 0$ .

Using the identity $\cos{3θ} = 4 \cos^3{θ} - 3 \cos{θ}$ , we get $2 \cos{3θ} + 1 = 0$ , so $θ = \frac{2\pi}{9}$ (any larger $θ$ that satisfies the equation causes $2θ$ to be greater than $90°$ , which doesn't work as the sum of the internal angles of $△BAD$ is greater than $4θ$ ).

Finally, since $△ABC$ is isosceles with $∠BAC = θ$ , $∠ABC = \frac{\pi}{2} - θ = \frac{5\pi}{18}$ , so our answer is $5 + 18 = \boxed{23}$ .

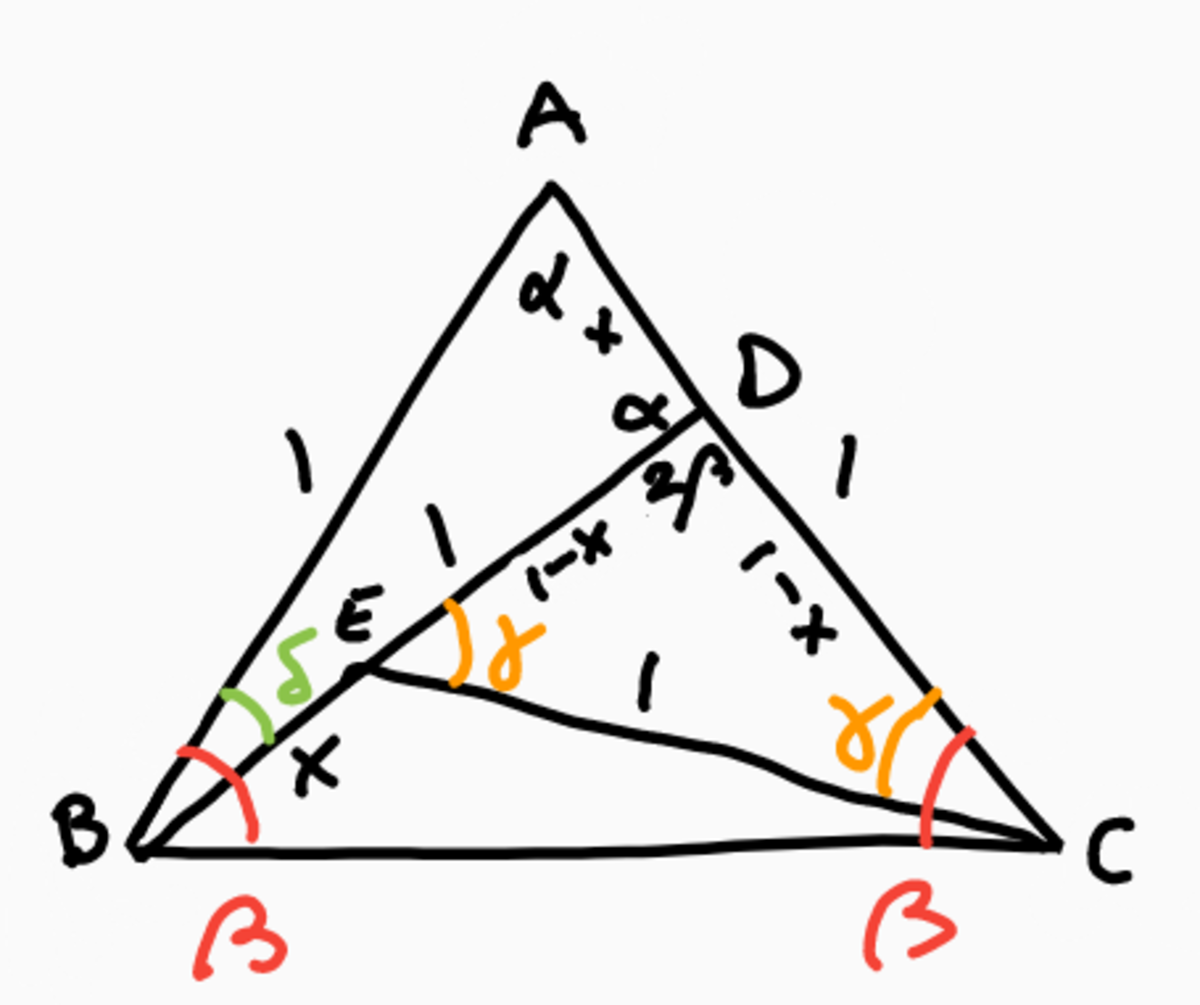
We have some isoscelese triangles:

• because $AB=AC$ we have $\angle ABC = \angle ACB = β$ , so that $\angle BAC = α = π-2β$
• because $AB=BD$ we have $\angle ADB = α$ , so that $\angle CDE=π-α=2β$
• because $DE=CD$ we have $\angle DCE= \angle DEC = γ$

Using the fact that the sum of angles in a triangle add up to π, we can easily find that

• $α=π-2β$
• $γ=\frac{1}{2}π-β$
• $δ=\angle ABD = π-2α = 4β-π$

Scale the diagram such that $AB=1$ . The cosine rule $c^2=a^2+b^2-2ab \cos φ$ can be applied to $\bigtriangleup ABD$ , so that, setting $x=AD$ , $x^2 = 2-2\cos (4β-π) = 2+2\cos 4β$ Via the identity $\cos 2t = 2\cos^2 t -1$ setting $t=2β$ , we get $x^2 = 4\cos^ 2β \Rightarrow x=|2\cos β|$ , and because $α,δ>0 \Rightarrow \frac{1}{4}π < β < \frac{1}{2}π\Rightarrow \cos 2β < 0$ , this means that $x=-2\cos 2β$ The cosine rule can also be applied to $\bigtriangleup CDE$ , so that $1^2 =(1-x)^2(2-2\cos 2β)$ Substituting $x$ with $-2\cos 2β$ , we obtain $-8\cos^3 2β+6 \cos 2β + 1 = 0$ Because of the identity $\cos 3t = 4\cos^3 t - 3 \cos t$ and setting $t=2β$ , we can rewrite this as $1-2 \cos(6β)=0$ which solves to $β= \frac{6k \pm 1}{18}π \text{ } (k \in \mathbb{Z})$

To satisfy both $0<x<1$ and $0<β<π$ we need $\frac{1}{4}π < β < \frac{1}{3}π$ , so that only $β= \frac{5}{18}π=50°$ is in this range and the answer is $5+18= \boxed{23}$ .